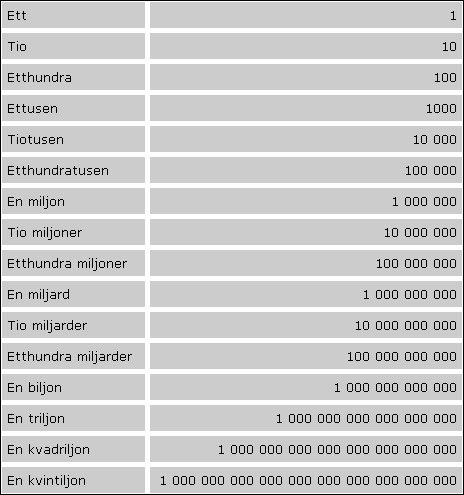
Vad är en miljard och hur många nollor har den?
Definition av miljard
En miljard är en siffra av monumental betydelse inom matematik och ekonomi. Det är ett tal som representerar tusen miljoner, vilket i numerisk form skrivs som 1 000 000 000. I det internationella systemet för numerisk representation är en miljard en del av den korta skalan, där varje steg innebär en multiplikation med tusen. Detta skiljer sig från den långa skalan som används i vissa länder, där en miljard skulle representera en miljon miljoner.
Denna distinktion är avgörande för att förstå hur stora tal hanteras och kommuniceras i olika kulturella och vetenskapliga sammanhang. En miljard används ofta för att beskriva befolkningsstorlekar, ekonomiska transaktioner och vetenskapliga mätningar, vilket gör det till ett grundläggande begrepp i både vardagligt och akademiskt språkbruk.
Antal nollor i en miljard
Att förstå antalet nollor i en miljard är en grundläggande aspekt av numerisk förståelse. En miljard består av nio nollor efter siffran ett, vilket kan illustreras som 1 000 000 000. Denna struktur är inte bara en matematisk formalitet utan en kritisk komponent i att förstå och arbeta med stora tal.
För att ytterligare fördjupa vår förståelse kan vi jämföra en miljard med andra stora tal. Till exempel har en miljon sex nollor (1 000 000), medan en biljon har tolv nollor (1 000 000 000 000). Denna progression av nollor är en del av den exponentiella tillväxten som definierar stora tal och är avgörande för att förstå deras relativa storlek och betydelse i olika sammanhang.
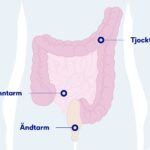 ont i nedre delen av magen man
ont i nedre delen av magen manStorleksordning av stora tal

Från miljon till biljon
Att navigera genom storleksordningen av stora tal är en fascinerande resa genom matematikens värld. Från miljoner till biljoner, varje steg representerar en exponentiell ökning i storlek och komplexitet. En miljon, som består av sex nollor, är ofta det första stora talet vi lär oss att förstå och använda. Det används i sammanhang som befolkningsstatistik och ekonomiska analyser.
När vi rör oss uppåt i skalan, kommer vi till miljarder, som vi redan har diskuterat, och sedan till biljoner, som har tolv nollor. Biljoner används ofta i vetenskapliga och tekniska fält för att beskriva enorma mängder, såsom avstånd i astronomi eller energimängder i fysik. Denna progression av tal är inte bara teoretisk utan har praktiska tillämpningar i många aspekter av livet och vetenskapen.
Triljon till deciljon
Vidare i vår utforskning av stora tal, når vi triljoner, kvadriljoner och vidare upp till deciljoner. Varje av dessa tal representerar en ytterligare multiplikation med tusen från det föregående talet. En triljon har 18 nollor, medan en kvadriljon har 24 nollor, och så vidare. Dessa tal används sällan i vardagliga sammanhang men är av stor betydelse inom vetenskap och teknik.
 kan man smitta om man har antikroppar
kan man smitta om man har antikropparFör att förstå dessa enorma tal kan vi använda dem i hypotetiska scenarier, såsom att beräkna antalet sandkorn på en strand eller antalet stjärnor i universum. Dessa övningar hjälper oss att greppa storheten och komplexiteten hos dessa tal och deras tillämpningar i verkliga världen. Att förstå dessa tal är en viktig del av avancerad matematisk utbildning och forskning.
Räkna nollor: En guide till stora tal
Praktiska exempel på stora tal
För att verkligen förstå stora tal och deras betydelse, är det viktigt att utforska praktiska exempel där dessa tal används. Till exempel, i finansvärlden, används miljarder och biljoner för att beskriva nationella budgetar och globala marknader. I vetenskapen används dessa tal för att mäta avstånd mellan galaxer eller energinivåer i kärnreaktioner.
Genom att använda konkreta exempel kan vi bättre förstå hur dessa stora tal påverkar vår värld. Till exempel, när vi diskuterar världens befolkning, som nu är över sju miljarder, kan vi börja förstå den skala och komplexitet som dessa tal representerar. Denna förståelse är avgörande för att kunna delta i globala diskussioner och fatta informerade beslut baserade på numeriska data.
Matematiska termer och deras betydelse
För att navigera i världen av stora tal är det viktigt att förstå de matematiska termer och begrepp som används för att beskriva dem. Termer som «exponentiell tillväxt», «logaritmisk skala» och «numerisk representation» är grundläggande för att förstå hur stora tal fungerar och hur de används i olika sammanhang.
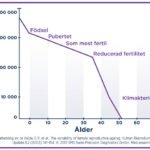 hur många ägg har en kvinna
hur många ägg har en kvinnaDessa termer hjälper oss att beskriva och analysera stora tal på ett exakt och meningsfullt sätt. Genom att förstå dessa begrepp kan vi bättre förstå de matematiska principer som styr vår värld och använda denna kunskap för att lösa komplexa problem och göra informerade beslut. Denna förståelse är en viktig del av matematisk utbildning och forskning, och hjälper oss att navigera i en värld där stora tal spelar en allt större roll.
Numerisk representation och talvärde

Hur man skriver stora tal
Att skriva stora tal korrekt är en viktig färdighet inom matematik och vetenskap. Det handlar inte bara om att placera rätt antal nollor efter en siffra, utan också om att förstå och använda rätt notation och symboler. Till exempel används vetenskaplig notation ofta för att representera mycket stora eller mycket små tal på ett kompakt och lättläst sätt.
Vetenskaplig notation använder sig av potenser av tio för att uttrycka stora tal. Till exempel, en miljard kan skrivas som 1 x 109. Denna metod är särskilt användbar i vetenskapliga och tekniska fält där precision och tydlighet är avgörande. Genom att behärska dessa tekniker kan vi kommunicera och arbeta med stora tal på ett effektivt och exakt sätt.
 skriva grattis på ett roligt sätt
skriva grattis på ett roligt sättNumerisk precision och noggrannhet
Numerisk precision och noggrannhet är avgörande när man arbetar med stora tal. Precision handlar om hur exakt ett tal är uttryckt, medan noggrannhet handlar om hur nära detta uttryck är till det sanna värdet. I många vetenskapliga och tekniska tillämpningar är det viktigt att balansera dessa två aspekter för att säkerställa korrekta och pålitliga resultat.
För att uppnå hög numerisk precision och noggrannhet används ofta avancerade matematiska tekniker och verktyg. Dessa kan inkludera datoralgoritmer, numeriska metoder och statistiska analyser. Genom att förstå och tillämpa dessa tekniker kan vi förbättra vår förmåga att arbeta med stora tal och fatta informerade beslut baserade på exakt och pålitlig data.
Matematiska begrepp relaterade till stora tal
Räkneprinciper och deras tillämpning
Räkneprinciper är grundläggande regler och metoder som används för att utföra matematiska operationer. Dessa principer är särskilt viktiga när man arbetar med stora tal, där små fel kan leda till stora avvikelser i resultatet. Genom att förstå och tillämpa dessa principer kan vi säkerställa att våra beräkningar är korrekta och pålitliga.
Några av de viktigaste räkneprinciperna inkluderar addition, subtraktion, multiplikation och division. Dessa operationer kan kombineras och manipuleras på olika sätt för att lösa komplexa problem och utföra avancerade beräkningar. Genom att behärska dessa principer kan vi förbättra vår förmåga att arbeta med stora tal och tillämpa matematiska metoder i olika sammanhang.
 hur kallt är det i rymden
hur kallt är det i rymdenNumerisk analys och forskning
Numerisk analys är en gren av matematiken som fokuserar på att utveckla och analysera algoritmer för att lösa numeriska problem. Denna disciplin är särskilt viktig när man arbetar med stora tal, där exakta analytiska lösningar ofta är omöjliga eller opraktiska att beräkna. Genom att använda numeriska metoder kan vi approximera lösningar och få insikt i komplexa problem.
Forskning inom numerisk analys är ett dynamiskt och växande fält som har tillämpningar inom många områden, inklusive fysik, ingenjörsvetenskap och ekonomi. Genom att utveckla och förbättra numeriska metoder kan vi förbättra vår förmåga att lösa problem och fatta informerade beslut baserade på exakt och pålitlig data. Denna forskning är avgörande för att driva framsteg inom vetenskap och teknik och för att förbättra vår förståelse av världen omkring oss.
Matematik i Sverige: Utbildning och resurser

Matematiklärare och deras roll
Matematiklärare spelar en avgörande roll i att forma framtida generationers förståelse och uppskattning av matematik. Deras uppgift är inte bara att undervisa i grundläggande matematiska koncept utan också att inspirera och engagera elever i ämnet. Genom att använda innovativa undervisningsmetoder och resurser kan lärare göra matematik tillgänglig och relevant för alla elever.
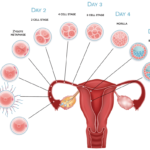 öka chansen att ägget fäster ivf
öka chansen att ägget fäster ivfI Sverige är matematiklärare viktiga aktörer i utbildningssystemet, och deras arbete stöds av ett brett utbud av resurser och program. Genom att delta i fortbildning och professionell utveckling kan lärare hålla sig uppdaterade med de senaste pedagogiska metoderna och forskningen inom matematikundervisning. Detta bidrar till att förbättra kvaliteten på matematikundervisningen och säkerställa att alla elever får en stark grund i ämnet.
Matematikböcker och undervisningsmaterial
Matematikböcker och undervisningsmaterial är viktiga verktyg för att stödja lärande och undervisning i matematik. Dessa resurser ger elever och lärare tillgång till en mängd olika övningar, exempel och teorier som hjälper till att fördjupa förståelsen av matematiska koncept. I Sverige finns det ett brett utbud av läromedel som är anpassade till olika nivåer och inlärningsstilar.
Genom att använda kvalitativa och engagerande läromedel kan lärare skapa en stimulerande inlärningsmiljö som uppmuntrar elever att utforska och förstå matematikens värld. Dessa resurser är också viktiga för att stödja självständigt lärande och ge elever möjlighet att utveckla sina färdigheter och intressen inom matematik. Genom att investera i bra undervisningsmaterial kan vi säkerställa att alla elever har tillgång till de verktyg de behöver för att lyckas i sina matematikstudier.
Matematikundervisning och lärande
Matematiklektioner och klasser
Matematiklektioner och klasser är kärnan i matematikundervisningen och utgör den primära miljön där elever lär sig och utvecklar sina matematiska färdigheter. Dessa lektioner är utformade för att introducera och förklara matematiska koncept, ge elever möjlighet att öva och tillämpa sina kunskaper, och uppmuntra kritiskt tänkande och problemlösning.
Genom att använda en mängd olika undervisningsmetoder och tekniker kan lärare skapa engagerande och effektiva lektioner som möter behoven hos alla elever. Detta inkluderar användning av visuella hjälpmedel, interaktiva aktiviteter och teknologibaserade verktyg för att förbättra inlärningen. Genom att skapa en positiv och stödjande lärandemiljö kan lärare hjälpa elever att utveckla en djup och varaktig förståelse för matematik.
Matematikprov och examinationer
Matematikprov och examinationer är viktiga verktyg för att bedöma elevernas förståelse och färdigheter i matematik. Dessa bedömningar ger lärare och elever möjlighet att identifiera styrkor och områden för förbättring, och de spelar en viktig roll i att informera undervisningsplanering och anpassning av undervisningsmetoder.
Genom att använda en mängd olika bedömningsmetoder, inklusive skriftliga prov, praktiska uppgifter och projektbaserade bedömningar, kan lärare få en omfattande bild av elevernas prestationer och framsteg. Detta hjälper till att säkerställa att alla elever får den stöd och vägledning de behöver för att lyckas i sina matematikstudier och förbereda sig för framtida akademiska och yrkesmässiga utmaningar.
Matematikproblem och lösningar

Vanliga matematikproblem
Matematikproblem är en integrerad del av matematikundervisningen och ger elever möjlighet att tillämpa sina kunskaper och färdigheter i praktiska situationer. Dessa problem kan variera från grundläggande aritmetiska uppgifter till mer komplexa algebraiska och geometriska utmaningar, och de hjälper elever att utveckla kritiskt tänkande och problemlösningsförmåga.
Genom att arbeta med en mängd olika matematikproblem kan elever förbättra sin förmåga att analysera och lösa problem, och de får en djupare förståelse för matematiska koncept och principer. Detta är en viktig del av matematikundervisningen och hjälper elever att förbereda sig för framtida studier och karriärer inom vetenskap, teknik och ingenjörsvetenskap.
Strategier för problemlösning
Att utveckla effektiva strategier för problemlösning är en viktig del av matematikundervisningen och hjälper elever att bli självständiga och kreativa tänkare. Dessa strategier kan inkludera att bryta ner problem i mindre delar, använda visuella hjälpmedel och diagram, och tillämpa logiska resonemang och deduktiva metoder.
Genom att lära sig och tillämpa dessa strategier kan elever förbättra sin förmåga att lösa komplexa problem och fatta informerade beslut baserade på matematiska data. Detta är en viktig färdighet som är användbar i många aspekter av livet och karriären, och det hjälper elever att utveckla en djup och varaktig förståelse för matematikens värld.
Matematikverktyg och applikationer
Programvara och plattformar för matematik
Moderna matematikverktyg och applikationer har revolutionerat sättet vi lär oss och tillämpar matematik. Programvara och plattformar som MATLAB, Mathematica och GeoGebra erbjuder kraftfulla verktyg för att utföra komplexa beräkningar, visualisera data och simulera matematiska modeller. Dessa verktyg är ovärderliga för både utbildning och forskning, och de hjälper användare att utforska och förstå matematiska koncept på djupet.
Genom att använda dessa verktyg kan elever och forskare förbättra sin förmåga att analysera och lösa problem, och de får tillgång till en mängd olika resurser och funktioner som stödjer deras arbete. Dessa verktyg är också viktiga för att främja samarbete och kommunikation inom matematikgemenskapen, och de hjälper till att driva framsteg inom vetenskap och teknik.
Matematikresurser online
Internet har öppnat upp en värld av möjligheter för att lära sig och utforska matematik. Online-resurser som Khan Academy, Coursera och EdX erbjuder gratis och tillgängliga kurser och material för att stödja matematikundervisning och lärande. Dessa resurser ger elever och lärare tillgång till en mängd olika övningar, videor och interaktiva verktyg som hjälper till att fördjupa förståelsen av matematiska koncept.
Genom att använda dessa online-resurser kan elever och lärare förbättra sin förmåga att lära sig och undervisa matematik, och de får tillgång till en mängd olika perspektiv och metoder som berikar deras inlärningsupplevelse. Dessa resurser är också viktiga för att stödja självständigt lärande och ge elever möjlighet att utforska sina intressen och passioner inom matematik.
Matematikgemenskap och nätverk

Matematikklubbar och föreningar
Matematikklubbar och föreningar spelar en viktig roll i att främja intresse och engagemang för matematik. Dessa organisationer erbjuder en plattform för elever och entusiaster att träffas, dela idéer och delta i aktiviteter och tävlingar som främjar matematikens värld. Genom att delta i dessa klubbar kan medlemmar utveckla sina färdigheter, utbyta erfarenheter och bygga nätverk med likasinnade individer.
I Sverige finns det många matematikklubbar och föreningar som erbjuder en mängd olika aktiviteter och evenemang för att stödja och inspirera matematikintresserade. Dessa organisationer är viktiga för att främja en positiv och stödjande gemenskap där medlemmar kan utforska och utveckla sina intressen och färdigheter inom matematik.
Forum och diskussioner om matematik
Online-forum och diskussioner om matematik erbjuder en plattform för att dela kunskap, ställa frågor och diskutera matematiska koncept och problem. Dessa forum är en värdefull resurs för elever, lärare och forskare som söker stöd och vägledning i sina studier och arbete. Genom att delta i dessa diskussioner kan medlemmar få insikt i olika perspektiv och metoder, och de kan bidra med sina egna erfarenheter och kunskaper.
Dessa forum är också viktiga för att främja samarbete och kommunikation inom matematikgemenskapen, och de hjälper till att driva framsteg och innovation inom fältet. Genom att delta i dessa diskussioner kan medlemmar bygga nätverk och relationer med likasinnade individer och bidra till att skapa en stark och stödjande gemenskap för matematikintresserade.
Matematikseminarier och workshops
Föreläsningar och presentationer
Matematikseminarier och workshops erbjuder en plattform för att dela och diskutera forskning, idéer och metoder inom matematik. Dessa evenemang inkluderar föreläsningar och presentationer av experter och forskare som delar sina insikter och erfarenheter med deltagarna. Genom att delta i dessa seminarier kan medlemmar få en djupare förståelse för aktuella trender och framsteg inom matematik och relaterade fält.
Dessa evenemang är också viktiga för att främja samarbete och nätverkande inom matematikgemenskapen, och de erbjuder en möjlighet för deltagare att lära sig av och inspireras av ledande experter och forskare. Genom att delta i dessa seminarier och workshops kan medlemmar förbättra sina färdigheter och kunskaper och bidra till att driva framsteg och innovation inom matematik.
Konferenser och symposium
Matematikkonferenser och symposium är viktiga evenemang som samlar forskare, lärare och studenter för att dela och diskutera forskning och idéer inom matematik. Dessa evenemang erbjuder en plattform för att presentera och diskutera ny forskning, metoder och tillämpningar inom fältet, och de ger deltagare möjlighet att lära sig av och inspireras av ledande experter och forskare.
Genom att delta i dessa konferenser och symposium kan medlemmar bygga nätverk och relationer med likasinnade individer och bidra till att skapa en stark och stödjande gemenskap för matematikintresserade. Dessa evenemang är också viktiga för att främja samarbete och innovation inom matematik och relaterade fält, och de hjälper till att driva framsteg och utveckling inom fältet.
Matematikfestivaler och utställningar
Evenemang för matematikentusiaster
Matematikfestivaler och utställningar erbjuder en unik möjlighet för matematikentusiaster att utforska och fira matematikens värld. Dessa evenemang inkluderar en mängd olika aktiviteter och utställningar som syftar till att inspirera och engagera deltagare i matematik. Genom att delta i dessa festivaler kan medlemmar lära sig om och utforska olika aspekter av matematik och dess tillämpningar i världen.
Dessa evenemang är också viktiga för att främja intresse och engagemang för matematik bland allmänheten, och de erbjuder en plattform för att dela och diskutera idéer och metoder inom fältet. Genom att delta i dessa festivaler och utställningar kan medlemmar förbättra sina färdigheter och kunskaper och bidra till att skapa en stark och stödjande gemenskap för matematikintresserade.
Utställningar och mässor
Matematikutställningar och mässor erbjuder en plattform för att visa upp och utforska olika aspekter av matematik och dess tillämpningar. Dessa evenemang inkluderar en mängd olika utställningar och demonstrationer som syftar till att inspirera och engagera deltagare i matematik. Genom att delta i dessa utställningar kan medlemmar lära sig om och utforska olika aspekter av matematik och dess tillämpningar i världen.
Dessa evenemang är också viktiga för att främja intresse och engagemang för matematik bland allmänheten, och de erbjuder en plattform för att dela och diskutera idéer och metoder inom fältet. Genom att delta i dessa utställningar och mässor kan medlemmar förbättra sina färdigheter och kunskaper och bidra till att skapa en stark och stödjande gemenskap för matematikintresserade.