NOVA ET ACCURATA
ASTROLABII
GEOMETRICI
STRUCTURA,
Ubi gradus, horumque singula minuta prima,
Nec non,
QUADRANTIS
ASTRONOMICI
AZIMUTHALIS,
Quo non solum prima, sed & singula minuta
secunda distinctè observari possunt.
UNA CUM
UTRIUSQUE USU,
Claris & Perspicius exemplis illustrato.
Operâ & studio
Benedicti Hedræi, Sueci.
Ra. Mtis Suecia stipend.

LVGDVNI BATAVORVM,
Ex Officina Wilhelmi Christiani Boxii.
Sumptibus Auctoris. 1643.
PATRICIUS
De Institutione Reipubl.
Lib. II.
Dimensionis disciplina artes singulus adjuvat,
Vix enim quidpiam agere possumus sine mensura.

SERENISSIMÆ, POTENTISSIMÆQUE
PRINCIPI AC DOMINÆ,
CHRISTINÆ
D.G.
SUECORUM, GOTHORUM,
VANDALORUMQUE DESIGNATÆ
REGINÆ
ET
PRINCIPI HÆREDITARIÆ,
MAGNÆ DUCI FINLANDIÆ,
DUCI ESTHONIÆ CARE-
LIÆQUE, DOMINÆ
INGRIÆ, &c.
REGINÆ
ET
DOMINÆ CLEMENTISSIMÆ.
S.æ R.æ M.tis
Regnorumque Sueciæ, Gothiæque, &c.
SENATORIBUS,
Quinque Viris Tutoribus & Administra-
toribus, Illustrissimis, Excellentissimisq;
Dominis,
- D. PETRO BRAHE, Comiti Wisings Borgh/ L. Baroni in Rydboholm/ & Lindholm/ Regni Suecia Archidapifero, suprimi Iudicii Regii, quod Holmia est, Presidi, Iudici provincialis Wesmannia & Dalecarlia.
- D. JACOBO DE LA GARDIE, Comiti in Lecköö/ L.B. in Eckholmen ; Domino in Kolcka/ Kyda/& Runßöö/ Equiti aurato, Regni Sueciæ Archimarchallo, Generali exercituum Præfecto, Collegii Bellici Præsidi, & Iudici Provinciali Vplandiæ.
- D. CAROLO CAROLI GYLLENHJELM/ L.B. in Bergqwara/ Domino in Sundbyholm/ & Kaßby/ Regni Sueciæ Architalasso, & Collegis Ammiralitatio Ræsidi, Iudici provinciali Smolandiæ.
- D. AXELIO OXENSTJERNA/ L.B. in Kimitho/ Domino in Fyholm & Tydöön/ Equiti aurato, Regni Sueciæ Cancellario, per Germaniam ad exercitus Legato, atque Evangelici fœderis ibidem Directori Generali, & Iudici provincialis Bothniæ Occidentalis.
- D. GABRIELI BENEDICTI OXENSTJERNA/ L.B. in Mörby & Lindholmen/ Regni Sueciæ Thesaurario & Iudici provincialis Wermelandiæ.
Dominis & Patronis magnis.

SERENISSIMA
POTENTISSIMAQVE
REGINA,
Illustrissimi atque Excellentissimi
HEROES,
 I tàm foret obvium
præstare quod Augusto
R.æ T.æ M.tis nomini debetur,
atque Illust. Excell.
vestr. gravissimo Sanctissimoque
judicio conveniret, quàm facilè
votis ad ea penetramus; non hîc mihi laborandum
esset quâ commendationis
gratiâ hanc emendatum Astrolabij & Quadrantis
Astronomici fabricam offerrem,
probaremque devotæ mentis cultum atque
humilimi obsequij fidem. Licet autem
illud omnibus ex æquo non sit distri-
I tàm foret obvium
præstare quod Augusto
R.æ T.æ M.tis nomini debetur,
atque Illust. Excell.
vestr. gravissimo Sanctissimoque
judicio conveniret, quàm facilè
votis ad ea penetramus; non hîc mihi laborandum
esset quâ commendationis
gratiâ hanc emendatum Astrolabij & Quadrantis
Astronomici fabricam offerrem,
probaremque devotæ mentis cultum atque
humilimi obsequij fidem. Licet autem
illud omnibus ex æquo non sit distri-
butum, cepi tamen consilium, sub auspicijs R.æ T.æ M.tis in publicum emittere laboris & studiorum meorum experimentum, atque sublimes Administrationis curas Illust. Excell. vestr. interpellare; non alia de causa, quàm ut haberet quo tueretur novitatem suam, sic-ubi adversam cæperit experiri fortunam: aut si ex voto successerit, non essem asymbolus numeroque tantum, arrodens publicam rem, nihil ad eam conferens labore vel industriâ. Omnia quæ complexu suo continet maxima illa terrarum orbis societas, moderatur supremus Imperator, varijs usibus aptando diversas ingeniorum propensiones, ut singuli aliquid conferant as salutem omnium, nisi nos ipsi destituamus, non eundo quò vocat Divini numinis ministra Natura, vel præter assignatas cuique partes, ad sublimiora enitendo. Unde non rarò accidit ut vel infrà subsistamus, vel rejecti ad propria, post factum discamus sapere. Sunt quibus maxima atque eximia quæque tribuit, ut tanquam Sol aut Luna inter cæteras eminerent orbis faces, & rerum tractatu à summi moderatoris magnitudine quam proximê abes-
sent. His alij succedunt ad singula plerumque ministeria adsciti, pro modo sua diffusam communis vitæ utilitatem sustinentes. Rectè atque ex usu publico se gerit, qui partes à natura datas tuetur. non enim satis merentur, ut in publicæ felicitatis s(?)ortem admittantur, qui otium discendis necessarijs impendi solitum, avertunt ad ignaviam & dissolutæ vitæ ignominiam. Quod malum, quò facilius occupat animos non dum firmatos boni iudicio, eò majori solicitudine cavetur in Regni, quæ R.a T.a M.as avito, non magis successionis jure, quàm piæ justæque dominationis exemplo moderaris, successu hostibus invidendo, optato amicis subditisque. Sic Lætissima capiunt incrementa cum progressu ætatis annorumque R.æ T.æ M.tis æquissimum domi imperium, foris armorum felicitas, ut spes s(?)it tandem non exigua restituendi orbis Europæi tranquillitatem, quam continuis fatigarus tumultibus, á R.a T.a M.te magno desiderio expectat. Deus qui supra nos humana curat, justæque causæ arbiter eventus rerum temperat, T.æ M.ti Serenissima REGINA, Imperium feliciter
in seros annos proferat prosperetque; vestram Illust. Excellentmiq; Domini mentem atque consilia dirigat & firmet ad Ecclesiæ pacem Patriæque salutem, pro quibus assiduo moleitoque Labore excubatis, ut diu benefici syderis aspectu fruamur, quod Septentrionem splendore Gustaviani sanguinis stupendæq: virtutis radijs illustrat. Quo voto me conatusque meos involuo, præsidij satis habiturus si R.æ T.æ M.ti vel animum tantum probatum dedero, qui in eo totus erit, ut sim
Serenissimæ R.a T.a M.ti
ad devotissima servitia
Illust. Excell. vestris
ad humilima obsequia
dicatissimus
subditus & cliens
B.Hedræus.

AUCTOR
Ad Lectorem.
 ON temerè susceptum est à me
negotium emendandi Astrolabium
Geometricum, sicut & Quadrantem
Astronomicum, quod scio in
multorum judicia incursurum. Quia supervacuum
dicent id tentare, quod vel ab aliis
tanquam desperatum est relictum, vel cui suprema
jam est imposita manus. Sed neutrum
potuit inhibere animum, quin perseveraret in
re tàm utili atque necessaria. Que etenim est
alia causa, quod toties contingat errare in usu
horum instrumentorum, quàm quod nobis in eorum
Fabrica & exacta divisione pollicemur. In puncto
enim vel minuto aliquo lapsus, longam trahit
erroris materiem, quod hærente semper scrupule,
crucem figere solet Matheseos studiosis.
Ideoque non putavi me præter rem facturum,
si inventis adderem, quod tractatu deprehenderem
vel necessarium, vel utile futurum ad
acuuratiorem horum Instrumentorum fructu-
ON temerè susceptum est à me
negotium emendandi Astrolabium
Geometricum, sicut & Quadrantem
Astronomicum, quod scio in
multorum judicia incursurum. Quia supervacuum
dicent id tentare, quod vel ab aliis
tanquam desperatum est relictum, vel cui suprema
jam est imposita manus. Sed neutrum
potuit inhibere animum, quin perseveraret in
re tàm utili atque necessaria. Que etenim est
alia causa, quod toties contingat errare in usu
horum instrumentorum, quàm quod nobis in eorum
Fabrica & exacta divisione pollicemur. In puncto
enim vel minuto aliquo lapsus, longam trahit
erroris materiem, quod hærente semper scrupule,
crucem figere solet Matheseos studiosis.
Ideoque non putavi me præter rem facturum,
si inventis adderem, quod tractatu deprehenderem
vel necessarium, vel utile futurum ad
acuuratiorem horum Instrumentorum fructu-
AD LECTOREM.
ram, huic labori tantum tribuens, quantum ratio & usus approbuverint.
Qui nunc accuratissimi Artifices habentur, non ulterius Astrolabia sua dividunt, quam gradum quemlibet in 6 partes æquales, ut quælibet earum valeat 10 minuta prima, cætera, quæ inter hæc divisionum puncta cadunt, conjecturâ tantum sunt inquirenda, qyæ res in ipsa praxi, magnos quandoque parit errores. In hoc vero Astrolabio, cujus fabrica hîc exhibetur, quàm exactissimè singula minuta prima haberi possunt, in Quadrante verò Astronomico, singula ferè secunda.
Sed dicu fortassè, Artifices sua instrumenta longè ulterius dividunt, quàm gradam quemlibet in 6 partes, lineæ quippè transversales huic divisioni inserviunt. Imò, fateor quosdam Artifices instrumenta sua per transversales has lineæs dividere, cujus divisionis experimentum etiam egomet feci, sed quàm sit fallax, & errori obnoxius iste dividendi modus, præsertim in parvis instrumentis, demonstratu non est difficile. Sit enim A B C D, pars limbi cujusdam instrumenti, ejus verò centrum E. Hanc limbi particulam volo per lineam trans-
AD LECTOREM.
versalem A C, in quator æquales dividere
partes. Divido ergò istam lineam A C, in
4 æquales partes in punctis F, G, H, ductis
per hæc puncta á centro E rectis, intersecabitur
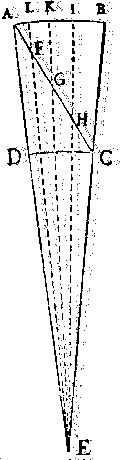 ijsdem arcus A B in punctis
L, K, I. Iam si hic modus dividendi
non esset erroneus, essent
omnes partes illius arcus, scil.
A L, L K, K I, I B, inter se
æquales, quod autem non sint æquales,
evide(?)ter ad oculum apparet,
& ex fundamentis tum opticis,
tum Geometricis facile demonstrari
potest. Nam etsi lineæ A F, F G,
G H, H C, omnes sint æquales,
quia tamen inæqualiter à centro
distant, inæquales etiam angulos
efficiunt. Item quò magis linea
aliqua in directum jacet, eò minorem
facit angulum sibi oppositum,
jam linea H G, non solum magis à centro
distat, quam C H, sed etiam magis in,
directum respectu ejusdem centri jacet. Nam
angulus G H E, externus, angulo H C E,
interno & opposito major est. Item angulus
ijsdem arcus A B in punctis
L, K, I. Iam si hic modus dividendi
non esset erroneus, essent
omnes partes illius arcus, scil.
A L, L K, K I, I B, inter se
æquales, quod autem non sint æquales,
evide(?)ter ad oculum apparet,
& ex fundamentis tum opticis,
tum Geometricis facile demonstrari
potest. Nam etsi lineæ A F, F G,
G H, H C, omnes sint æquales,
quia tamen inæqualiter à centro
distant, inæquales etiam angulos
efficiunt. Item quò magis linea
aliqua in directum jacet, eò minorem
facit angulum sibi oppositum,
jam linea H G, non solum magis à centro
distat, quam C H, sed etiam magis in,
directum respectu ejusdem centri jacet. Nam
angulus G H E, externus, angulo H C E,
interno & opposito major est. Item angulus
AD LECTOREM.
F G E externus, major est interno & opposito G H E. Et sic de omnibus quotcunque essent, dicendum foret. Hinc apparet, quod ubique duplex sit causa, cur anguli ad centrum E, & per consequens partes in arcu A B, inæquales evadant. Nam quæcunque pars lineæ transversalis magis à centro distat, eadem etiam magis in directum jacet, ideo(?) nec mirum est, quod partes iste A L, L K, K I, I B, que æquales esse deberent, maximè æquales fiant.

Prætereà etiam ex prop. 3. lib.6. Eucl. eorundem angulorum ad centrum inæqualitas demonstrari potest. Nam si recta, quæ trianguli angulum bifariam secat, secet etiam basim; habebunt segmenta baseos eandem inter se rationem, quam habent latera circa angulum bisectum. Sit itaque in adjecta figura, pars limbi M N, bifariam dividenda per lineā transversalem M O, si jam ista linea pro more dividatur in duas partes æquales in puncto Q, per
AD LECTOREM.
quod à centro P ducatur recta P Q, dico angulos M P Q, & Q P O, esse inäquales, quia partes baseos M Q & Q O, non habens eam rationem inter se, quam habent latera O P & P M, dividatur ergo M O, secundum rationem Laterum O P & P M, in puncto R, & ducatur P R, secabit illa angulum O P M, bifariam, & simul etiam ostendet inæqualitem angulorum O P Q & Q P M.

Si tamen modus iste per lineas transversales esset retinendus, curvæ lineæ, non rectæ essent adhibendæ. Curvitas autem ista inveniri potest, si per tria puncta, ut in apposita figura, S, T, V, ducatur arcus, Cujus pars scil. S T, in particulas æquales est dividenda, lineæ enim à centro per ista puncta transeuntes, dividunt peripheram in partes æquales, quod prop.27. lib.3. Euclid. demonstratur.
Si autem quis dixerit non opus esse in rebus Geometricis tàm accurato instrumento, ut singula minuta habeantur, sufficere decima quæque haberi,
AD LECTOREM.
Cætera facile per conjecturam, quoad opus
fuerit, notari possunt: Sed quàm in Geometria
sit accuratio hæc necessaria, unico tantum
exemplo ostendam : Sit distantia A B inquiperticarum,
 renda ex cognita basi A C 100.
angulus ad A est
rectus, angulum vero ad C sit
89°.13'. Dico itaque, ut 100000.
ad 7313899. (tangentem scil.
anguli 89°.13'.) ita A C 100.
ad 7314. quæ erit vera distantia
quæsita. Ponamus autem
observatorem unico minuto aberrasse
in observatione istius anguli
ad C, & illum posuisse 89°.12'.
operatione peractâ, proveniet pro
distantia A B, 7161. quâ à vera
distantia 7314. subtractâ, relinquuntur
153. pert. Si itaque
153. pert. à vera distantia aberraverit,
unico tantum minuto neglecto; quantus
quæso erit error, si 3, 4, vel 5, minuta
(quod facilimè in vulgaribus instrumentis fierè
potest) negligantur? Unde patet, quam etiam
necessarium sit Geometram accuratum habere
renda ex cognita basi A C 100.
angulus ad A est
rectus, angulum vero ad C sit
89°.13'. Dico itaque, ut 100000.
ad 7313899. (tangentem scil.
anguli 89°.13'.) ita A C 100.
ad 7314. quæ erit vera distantia
quæsita. Ponamus autem
observatorem unico minuto aberrasse
in observatione istius anguli
ad C, & illum posuisse 89°.12'.
operatione peractâ, proveniet pro
distantia A B, 7161. quâ à vera
distantia 7314. subtractâ, relinquuntur
153. pert. Si itaque
153. pert. à vera distantia aberraverit,
unico tantum minuto neglecto; quantus
quæso erit error, si 3, 4, vel 5, minuta
(quod facilimè in vulgaribus instrumentis fierè
potest) negligantur? Unde patet, quam etiam
necessarium sit Geometram accuratum habere
AD LECTOREM.
instrumentum, quo singula minuta distinctè observare possit. Quare si quid profecero, utere fruere tuo bono. Ego neque alijs invideo si quid rectius fieri judicaverint, neque, si res postulat, monitorem defugio,
Vale.


Ne dicat quispiam cum Platone Ideas me delineaste, expertum subindicabo Artificem, qui ad divisionem hanc meam accuratum mihi confecit Astrolabium; Ultrajecti est f Snee Wins, qui experientiâ in alijs instrumentis Mathem. fabricandis summè laudandâ, & in hoc, cujus hîc descriptionem exhibeo, industria singulam. Huic igitur si res committatur, quid præstitum sit, apparebit.

(1)

PARS PRIMA
DE
ASTROLABIO.
Membrum I.
De ejus Fabrica.
Cap. I.
De Adornatione Lìmbi.
 Iat ex lamina Orichalcea rudimentum
quoddam, prout solet
fieri pro Astrolabio vulgari fabricando,
constans scil. limbo & duabus
diametris ad angulos rectos sibi
insistentibus, sed aliguantò majoris crassitiei, spatioque
in medio pro compasso relicto. Huic limbo
immergatur circulus quidam, ita ut unum cum eo
constituat planum, & æqualiter in eo moveri &
circumduci possit. Crassities hujus circuli sit (?)
crassitiei limbi, Latitud tanta, ut commodè dividi
possit in tres partes, quarum una divisiones,
duæ reliquæ duos numerorum ordines continebunt,
de quibus in sequentibus plura.
Iat ex lamina Orichalcea rudimentum
quoddam, prout solet
fieri pro Astrolabio vulgari fabricando,
constans scil. limbo & duabus
diametris ad angulos rectos sibi
insistentibus, sed aliguantò majoris crassitiei, spatioque
in medio pro compasso relicto. Huic limbo
immergatur circulus quidam, ita ut unum cum eo
constituat planum, & æqualiter in eo moveri &
circumduci possit. Crassities hujus circuli sit (?)
crassitiei limbi, Latitud tanta, ut commodè dividi
possit in tres partes, quarum una divisiones,
duæ reliquæ duos numerorum ordines continebunt,
de quibus in sequentibus plura.
(2)
Hic circulus ita suæ foveæ inhærebit, ut inde
non excidat, quomodocunque vertatur instrumentum.
Quod vel beneficio aliquot cochlearum
fieri potest, v.g. in figur apposita, sit pars limbi
 A B C D, pars v. circuli mobilis E F C D, G. v.
sit foramen ubi dioptra collocanda erit. Solent
a. in angulus circa dioptras relinqui spatia quædam,
ut H I, in quibus spatiis non incommodè
poni possunt cochleæ, quæsuo ambitu nonnihil
circulo mobili incumbant, sicut ad K videre est.
Vel etiam si pars limbi, quæ extrâ hunc circulum
est, componatur ex duabus Lamellis, potest enim
tunc circulus ita præparari, ut excidere non possit.
ut si intelligatur limbus cum circulo ímmerso di
A B C D, pars v. circuli mobilis E F C D, G. v.
sit foramen ubi dioptra collocanda erit. Solent
a. in angulus circa dioptras relinqui spatia quædam,
ut H I, in quibus spatiis non incommodè
poni possunt cochleæ, quæsuo ambitu nonnihil
circulo mobili incumbant, sicut ad K videre est.
Vel etiam si pars limbi, quæ extrâ hunc circulum
est, componatur ex duabus Lamellis, potest enim
tunc circulus ita præparari, ut excidere non possit.
ut si intelligatur limbus cum circulo ímmerso di
 scendi ad angulos rectos,
erit sectio ejus
L M N O, sectio v. circuli
mobilis Q R S T,
scendi ad angulos rectos,
erit sectio ejus
L M N O, sectio v. circuli
mobilis Q R S T,
(3)
qui inferior fui parte ad S, superioré quæ est ad R suo ambitu aliquantulum excedat. Circulo sic præparato limboque imposito, adjungatur alius circulus, cujus sectio est R S V M, qui limbo immobili claviculis vel cochleis est affigendus. Atque sic etiam circulus mobilis semper in suo loco manebit.
Debet autem hic circulus, præsertim parte sua exteriore, tàm concinnè cum limbo congruere, ut videatur esse cum eo continuum quid, ita tamen ut facile absque violentia circumduci possit.
Circulo hoc ita immerso, & toto limbo unà cum circulo totno vel aliis instrumentis quàm exquisitissimè elaborato, ut appareat tanquaam una superficies plana & continua, ductis ex centro aliquot circulis, quibusdam extra hunc circulum in limbo immobili, quibusdam in ipso circulo, prout requirunt divisiones & numerorum ordines utque in ipsa delineatione apparet, tunc fir(?)metur iste circulus pice vel bitumine vel alio quocunque moddo, ut ita immobilis persistat, donec instrumentum, ad eum modum, quem jam visuri sumus, fuerit divisum.
Cap. II.
De hujus Instrumenti Divisione.
DUcantur per centrum ad angulos rectos duæ lineæ rectæ, quæ & limbum & circulum mobilem in quatuor quadrantes omninò æquales dividant.
Deinde spatium illud in limbo exteriori, quod proximè adiacet circulo mobili, dividatur more
(4)
solito quilibet nempè quadrans in 90. partes æquales. Sed hic omnis cura & diligentia est adhibenda, ut omnes istæ partes omnino fiant æquales inde enim tota perfectio instrumenti dependet.
Limbo sic diviso, numerentur ab una linearum, quas vocant fiduciæ, ut in delineatione A B, in quam partem placuerit, 61. gr. ab A, usque in C, & spatium illud in circulo mobili, quod hisce 61. gr. respondet, dividatur in 60. partes æquales, in qua divisione, non minor adhibenda est cura, quam in divisione Limbi.
Quia autem tota Latitudo circuli mobilis divisa sit in tria spatia (ut priùs dictum est) quorum duo interiora erunt pro numeris inscribendis, tertium v. & exterius, quod limbum jam antea divisum proximè attingit, Capiat prædictas 60. partes. Cavendum est diligenter, ne inter dividendum Limbum, graphio attingatur circulis mobilis, & dum dividetur circulus, ne attingatur limbus, ita ut aliqua vestigia remaneant, quæ deinceps in observationibus impedimento fuerint. Notandum & hoc est, quod ambæ istæ divisiones non debeant fieri per rudes & crassas, sed per æquales & subtiles lineas.
Divisione sic absolutâ, dimittatur iterum circulus, ut liberè in quamcunq; partem moveri & circumagi possit, & jam explorandum est, num rectè divisum sit Instrumentum nec ne, quod certè accuratissimè ac perfectissimè fieri potest hoc modo.
Cap. III.
De Divisionis Examine.
MOveatur circulus in quamcunque partem placuerit, ita ut una linea extremarum ex-

(5)
actè congruat cum aliqua linea in limbo immobili, tum vide num & altera extrema quoque cum aliqua linea in Limbo conveniat, quod si fuerit, benè est, sin minus, erratum. Ubicunque enim una extremarum exactè cum aliqua linea in limbo concurrit, necessariò etiam id fiet in altera, si modo erratum non fuerit.
Et concordantibus extremis, nulla unquam intermediarum concordabit, nisi error fuerit commissus. Hoc aliquoties (quò sæpius, eò melius) repetito, si nullus deprehensus fuerit error, indicium est bonæ & perfectæ divisionis.
Deindè moveatur circulus ita, ut lineæ extremæ cum aliis non concordent, & diligenter inspiciantur lineæ intermediæ, si tum plures quàm una earum deprehendantur congruere, vitiosè divisum est instrumentum. Nunquam enim plures quam una congruere possunt, quando extremæ non congruunt.
Aliquando contingere potest, ut nulla linea exactè cum alia conveniat, sed duæ proxime videntur ambæ qusi convenire, neutra tamen exactè, quod quando in praxi contingit, tunc præter minuta prima, quæ una earum indicat, etiam 30. minuta secunda denotantur.
Hinc facile apparet, quàm hoc Instrumentum examinari potest accuratissimè, ut si vel hilum inter dividendum aberratum est, illud hoc examine abhibito, statim ad oculum appareat.
Si quis adhuc ulterius examen requirat potest illud sic habere: Absolutâ prius dictâ divisione circuli, cum is adhuc firmatus persistit, sumatur etiam in opposita parte tale spatium, quod scil. 61. gradibus Limbi respondet, illudque dividatur ut prius, in 60. partes æquales, tunc enim in exami-
(6)
ne, quocunque volvatur circulus, quæ linea in uno spatio concordat, eadem semper (id est, ordine eadem) etiam in altero spatio concordabit. v. g. si in uno spatio concordat linea 20. etim linea 20. in altero concordabit si 25. in uno, etiam 25. in altero. & sic in cæteris. si enim eadem ordine linea utrobique non semper congruerit, instrumentum vitio non caret.
Prodest etiam circulum ita in duabus oppositis partibus dividere, ob majorem facilitatem in ipsa praxi; sic enim angulum observatum, sive in aversa, sive adversa parte numerare placet, licebit. Anguli enim ad verticem semper sunt æquales. Et commodius est angulum oppositum inspicere, & in eo gradus & minuta numerare, quia is semper est proximior, & ab omni impedimento liber. Propterea etiam dioptras interius, & divisiones exterius dispositas volui, ne dioptræ observatori, in numerandis anguli observati partibus, sint impedimento.
Possunt etiam plura spatia in circulo, modo prædicto, dividi, si ita visū fuerit, nempè ab altera parte istius lineæ, ubi prior divisio incepit, & in contrariam partem procedet. In praxi tamen, quot gradus & minuta in uno spatio denotantur, totidem etiam in reliquis omnibus denotari debent, si erratum non fuerit.
Cap. IV.
De Numeris.
INstrum. sic diviso & examinato, apponēdi sunt numeri, primò in Limbo immobili incipien-
(7)
do ab una linearum Cardinalium, & signandus decimus quisque gradus lineolâ paululum productâ, ubi ponendi sunt numeri 10. 20. 30. &c. usque ad 180. Inde vicissim retrò procedet alius numerorum ordo, 10. 20. 30. &c. usque ad 180. ut prius. Eodem modo fiat in altero semicirculo.
Deinde ìn circulo mobilì, simli modo notentur decimæ quæcunque particulæ, incipiendo ab una extremarum, qua placuerit, his numeris: 10. 20. 30. &c. ut in ipso schemate facile videre licet.
Usus horum numerorum est, ut gradus & minuta in observationibus indicent. Et quidem numeri in limbo gradus, numer v. in circulo minuta demonstrant. Itaque quando anglum aliquem observaveris, statim inspice lineam fiduciæ in circulo mobili, quæ dioptræ subiacet, si ea exactè convenit cum aliqua linea in limbo, tunc tantum gradus denotantur, & nulla minuta. Et numerus in limbo huic lineæ appositus indicabit quot graduum sit angulus iste. Si verò dicta linea fiduciæ non conveniat cum aliqua linea in limbo, tum in primis attende quot gradus integros ista linea sit prætervecta, illos memoriâ teneto; deinde inspice circulum mobilem, & quære in eo lineam quæ exactè alicui lineæ in limbo respondeat, numerus huic lineæ in circulo appositus, indicabit quot minuta præter gradus in limbo notatos, angulus observatus contineat.
Sed hoc diligenter notandum est, quod minuta semper in contrariam partem, respectù graduum, sint numeranda. hoc est, si gradus numerantur à dextra sinistrorsum, tunc minuta à sinistra dextror-
(8)

sum numeranda sunt, & contrà, si numeratio graduum procedit à sinistra, procedet nn(sic)meratio minutorum à dextra.
Quod autem partes istæ in circulo mobili reverà minuta denotent, sic ostendo: Sit A B in figura apposita, pars limbi immobilis continens 61. gradus, C D v. pars circuli mmobilis, in 60. partes æqualesdivisa. Cum itaq; ille idem angulus, qui cōtinet 61. gr. divisus sit in circulo in 60. partes æquales, manifestum est, quamlibet partem circuli mobilis continere unum gradum & unum minutum primum. Nam si dixero: 60. partes in circulo, dant 61. gr. in limbo, quantum dat una pars ejusdem circuli? operatione peractâ, proveniet in quoto unus gradus & unius gradus, id est, unum minutum primum. Hoc ostenso, quod quælibet pars circuli contineat unum graum & unum minutum, sequitur quod duæ partes ejusdem contineat duos gradus & duo minuta, tres partes,
(9)
3. gr. & 3. minuta, & sic consequenter usque ad divisionis finem, ubi 60. partes circuli continent 60. gr. & 60. minuta, id est, 61. gr.
Congruentibus jam extremis, ita ut A C, s(?)it una linea recta, & B D similiter una recta, & prima linea ab hac in limbo, scil. F, denotat unum gradum; prima v. linea in circulo scil. E, denotat unum gradum & unum minutum, ut ostensum est, non debent ergò exactè congruere, sed tanto discrepare spatio, quantum uni minuto tribuendum sit. Linea autem G notata, tanto distare ebet spatio à linea H, quantum duobus minutis tribuitur, Sic linea notata litera I, qn(sic)æ in ordine est decima, 10. minutis à linea K, distare debet. Et sic de omnibus aliis, quota enim quælibet inordie sit, tot minutis à sequenti in limbo linea distare intelligitur. Concipiamus jam circulum C D, moveri ab A versus B, tantum ut linea E coincidat cum linea F, erit tunc circulus iste per unum saltem minutum promotus.
Si verò tantum moveatur, ut G cum H conveniat, per duo minuta motus erit. Si autem linea I, respondeat lineæ K, per decem minuta tunc erit devolutus. Ponamus autem quod tantum promotus sit circulus, ut linea L, respondeat lineæ M, tunc 47. minuta pertransivit, est enim linea ista in ordine quadragesima septima. Et sic de cæteris.
Eadem prorsus ratio est, si intelligatur idem circulus moveri à B versus A. Et tunc minutaa in contrariam partem, à C nempe versus D, sunt numeranda, ut antea dictum est.
(10)
Cap. V.
De Dioptris.
VAriis quidem modis dioptræ adornari possunt,
omissis tamen aliis, modū hunc præserendum
censeo, quo tota dioptra in duas, dividitur
partes, in quarum una fiat rimula quædam tenuis,
in altera v. parte, magnum quoddam foramen,
in cujus medio subtile quoddam statuatur
filum, ut in delineatione apparet. Illud autem foramen
sive sit rotundum, sive quadrangulare, sive semicirculare;
perinde fuerit. Existente rimula in
superiori parte in una dioptra, tum in opposita dioptra
similis rimula in inferiori parte esse debet, ut
 semper rimulæ unius dioptræ directè respondeat
filium in foramine dioptræ alterius. prout ex adjectis
figuris colligere licet.
semper rimulæ unius dioptræ directè respondeat
filium in foramine dioptræ alterius. prout ex adjectis
figuris colligere licet.
Solent quidem communiter sex constitui dioptræ, quatuor in limbo immobili, & duæ in Requla moblii, sed in hoc Instrumento, meo quidem
(11)
judico, sufficunt quatuor, duæ in limbo immobili ad opposita partes, & duæ in circulo mobili, etiam in partibus oppositis.
Nam sæpè in praxi contingit, ut observandus angulus, vel sit recto paulò minor, vel etiam paulò ,ajor, in ejusmodi casibus, angulus difficulter obsservari potest, si sex fuerint dioptræ, quia duæ istæ in limbo, reliquis duabus in Regula sunt impedimento. Ubi v. duæ tantum dioptræ in limbo fuerint, angulus quicunque oblatus, absque omni impedimento observari potest.
Quando autem angulus rectus vel observandus vel constituendus sit, moveatur circulus mobilis, donec ejus linea fiduciæ, cui dioptra insistit, exactè coincidat cum linea Cardinali in Limbo. ubi nulla est dioptra, & sic de rectitudine anguli dubitari non potest.
In affigendis autem dioptris, quam diligentissimè cavendum est, ne filum vel rimula in dioptra cadat extrà lineam fiduciæ, si enim ista linea non exactè & directè subsit filo, & filum rimulæ, instrumentum non erit perfectum.
Præter has dioptras, conficiendæ sunt adhuc duæ aliæ (dua enim sufficiunt) ad altitudinem circiter semipedis, quæ prioribus dioptris, quando res postulat, superimponi possunt, & cochleâ ibi firmari. Quando enim planum non est æquale, sed vel sursum vel deorsum vergit, tunc adhibendæ sunt hæ dioptræ, & quidem si sursum collimandum erit, tunc collocandæ sunt in aversa parte instrumenti. Si v. deorsum; in proxima parte sunt ponenæ.
(12)

commodissima hæc videtur, ut tota dioptra dividatur in aliquot partes æquales, pro lubitu, quatuor, quinque sex &c. plures vel pauciores, & in alternis partibus fiant rimulæ, in partibus v. intermediis, magna fiant foramina quorum quodlibet in medio Subtile habebit filum, ut ante. Hæc melius ex inspectione figuræ, quam longis verborum ambagibus intellligi possunt.
(13)
Cap. VI.
De alijs modis Instrumenta dividendi.
POssunt & hujusmodi instrumenta aliis multis & variis modis, pro varia eorum quantitate dividi. Si enim instrumentum tam magnum fuerit, ut commodè quilibet gradus in duas partes dividi possit, atque sic totus limbus in 720. partes æquales. Si jam spatium in circulo mobili, quod 61. hujusmodi partibus respondet, dividatur in 60. partes æquales, tum præter gradus & singula minuta prima, etiam minuta dimidia, sive 30. minuta secunda observari possunt. Si v. spatium quod 31. partibus respondet distribuatur 30 partes æquales, habebuntur tantum singula minuta prima. Quod si v. spatium quod 16. partibus respondet, divisum fuerit in 15. partes æquales, dabuntur tunc bina quælibet minuta prima. Quando v. instrumenti limbus totus dividitur in 360. partes æquales, ut antea dictum est, & communiter fieri solet, si tum spatium in circulo, quod 31. gradibus limbi respondet, divisum fuerit in 30 partes æquales, notabit quælibet lineola duo minuta prima. Si spatium, quod 16. gradibus respondet, dividatur in 15. partes æquales, dabit quælibet linea 4. minuta prima.
In minoribus autem instrumentis, si totus limbus dividatur tantum in 180. partes æquales, ita ut quælibet pars valeat duos gradus. Si tunc spatium quod 61. hujusmodi partibus respondet, in 60. partes æquales distribuatur, valebit quælibet pars duo minuta prima. Si v. spatium quod 31. partibus respondet, dividatur in 30 partes æqua-
(14)
les, dabit quælibet pars minuta quatuor. His benè intellectis, facile quivis ingeniosus modos plures ex se ipso excogitare potest. De magnis verò instrumentis Astronomicis, dicetur suo loco.
Compassus, Pes, item Armilla, quâ instrumentum in quamcunque partem flecti & reflecti possit, construantur eo modo, quo fieri conveverunt.
Cap. VII.
De Transportatore.
TAli instrumento, quod jam descriptum est, acquisito, si quis angulos omnes satis accuratè in gradibus & minutis observaverit & annotaverit, non habuerit v. instrumentum, quo iidem in Chartam transferri possunt, ea scil. accuratione, quâ observavit, & angulos observavit. Itaque nunc dispiciendum est de ejusmodi instrumento, quo id commodè fieri potest. Tale instrumentum Transportatorem seu Transporteur vocant, intellige semicirculum in 180 gradus divisum. Ut autem hoc instrumentum ex iis fundamentis construatur, quinus ipsum Astrolabium confici dictum est, non semicirculus, sed integer circulus assumendus est, sujus dimidium exscidendum est, ita tamen ut relinquatur limbus quidam, quemadmodum in vulgaribus instrumentis fieri solet, & in adjecta figuratione apparet.
Extra hunc limbum fiar circulus, qui circa eum in qamcunque partem æqualiter moveri possit, & sit ejusdem cum limbo crassitiei, ita ut &
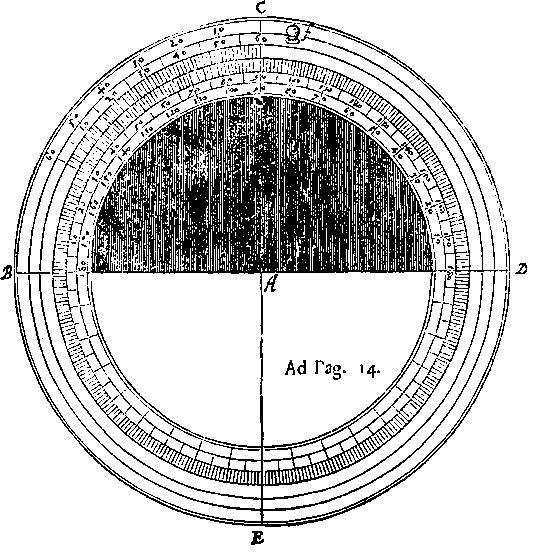
(15)
suprà & infrà idem cum illo constituat planum.
Debet autem hic circulus limbò ita adjungi, ut
non excidat, & ab eo separetur, quod quidem aliquam
difficultatem præ se ferre videtur, id tamen
facilè fieri potest, si & instrumentum ipsum, &
circulus, qui moveri debet, conficiantur ex duabus
diversis lammelis, iisque quantum fieri potest,
tenuibus & æqualiter explanatis, possunt enim
tunc ita adornari & conjungi, ut circulus ab instrumento
non divellatur, sed semper eidem adhæreat.
ut in subjecta figura, si intelligatur instrumentum,
una cum circulo mobili in duas discindi partes,
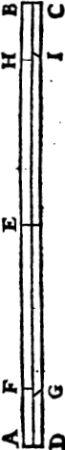 erit planum istius sectionis
A B C D, centrum instrumenti E,
quia sectio per centrum transire intellìgitur.
sectio circuli mobilis ab
una parte A F G D, ab altera v. parte
H B C I, A B sit pars instrumenti
superior, D C v. inferior. Iam circa
F G & H I, facile apparet qualis
esse debeat junctura, quâ circulus
cum ipso instrumento jungatur. Si
hac ratione circulus cum instrumento
connectatur, ab eo separari
non potest. Instrumento sic cum circulo
confecto, & benè in utraque
parte superiori scil. & inferiori explanato,
firmetur circulus, & instituatur
divisio eodem prorsus modo,
quo Astrolabium divisum est, totus
scil. limbus in extima ora, quâ circulum
attingit, in 360 partes æquales,
& spatiū in circulo mobili, quod
61. gradibus respondet, in 60 partes
æquales. Qui v. contentus est mi-
erit planum istius sectionis
A B C D, centrum instrumenti E,
quia sectio per centrum transire intellìgitur.
sectio circuli mobilis ab
una parte A F G D, ab altera v. parte
H B C I, A B sit pars instrumenti
superior, D C v. inferior. Iam circa
F G & H I, facile apparet qualis
esse debeat junctura, quâ circulus
cum ipso instrumento jungatur. Si
hac ratione circulus cum instrumento
connectatur, ab eo separari
non potest. Instrumento sic cum circulo
confecto, & benè in utraque
parte superiori scil. & inferiori explanato,
firmetur circulus, & instituatur
divisio eodem prorsus modo,
quo Astrolabium divisum est, totus
scil. limbus in extima ora, quâ circulum
attingit, in 360 partes æquales,
& spatiū in circulo mobili, quod
61. gradibus respondet, in 60 partes
æquales. Qui v. contentus est mi-
(16)
nutis quibuslibet binis, dividat totum limbum in 180 partes æquales, & spatium, quod 61 ejusmodi partibus respondet, in 60 partes æquales, dabit quælibet pars duo minuta prima.
Circulo mobili claviculus quidam infigi potest, ut in Schemate ad F, quo apprehenso, circulus pro arbitrio circumduci potest.
Num rectè divisum sit, eodem modo explorari potest, ut suprà.
Applicatio hujus instrumenti non multum differt ab applicatione vulgaris. Linea enim B D, applicanda est unilateri anguli dati, ita ut centrum A præcisè respondeat puncto angulari, deinde moveatur circulus, donec punctum C, id est, extremitas lineæ A C, exactè coincidat cum reliquo latere, tunc eadem linea indicabit anguli gradus in limbo, minuta autem in circulo mobili sunt quærenda, idque in contrariam partem, ut suprà Cap. 4. dictum est.
MEMBRUM II.
DE
ASTROLABII USV.
Problema I.
Altitudinem rei accessibilis metiri.
 It altitudo investiganda A B, sumatur
ergò locus quicunque, v. g. in C, ibique
collocetur Astrolabium ad perpendicu-
It altitudo investiganda A B, sumatur
ergò locus quicunque, v. g. in C, ibique
collocetur Astrolabium ad perpendicu-
(17)
lum, deinde moveatur circulus mobilis, donec per
illius dioptras conspiciatur summita altitudinis,
 A, hoc facto, inspiciendus
est instrumenti limbus,
& videndum quot
gradus contineantur, inter
lineam horizonti parallelam,
& lineam fiduciæ
circuli mobilis,
quæ directè medio dioptræ
substat, sint e. g.
inventi 64 gr. integri &
aliquid ultrà, itaque ab
eadem retrò numerandum
est, donec perventum
fuerit ad aliquam
lineam in circulo mobili,
quæ exactè congruat
cum linea aliqua B
in limbo immobili, sit ea v. gr. 48. quæ totidem
minuta denotat. Erit ergò angulus A C B, 64.48'.
Cn(sic)m hoc invento angulo ingrediendum est
tabulas sinuum (quarum cognitionem in toto hujus instrumenti
usu præsupponi necessum est) & videndum
quis sit numerus tangentis talis arcus, nimirum
212510. Distantia v. inter locum C, & fundamentum
altitudinis B, investiganda est catenâ,
funiculo, vel aliâ mensurâ, sitque ea 40 part erit
ergò per Regulâ proport. ut 100000. ad 212510;
ita 40. ad altitudinem quæsitam, quæ peractâ
operatione, erit 85. partium talium, qualium distantia
B C est 40.
A, hoc facto, inspiciendus
est instrumenti limbus,
& videndum quot
gradus contineantur, inter
lineam horizonti parallelam,
& lineam fiduciæ
circuli mobilis,
quæ directè medio dioptræ
substat, sint e. g.
inventi 64 gr. integri &
aliquid ultrà, itaque ab
eadem retrò numerandum
est, donec perventum
fuerit ad aliquam
lineam in circulo mobili,
quæ exactè congruat
cum linea aliqua B
in limbo immobili, sit ea v. gr. 48. quæ totidem
minuta denotat. Erit ergò angulus A C B, 64.48'.
Cn(sic)m hoc invento angulo ingrediendum est
tabulas sinuum (quarum cognitionem in toto hujus instrumenti
usu præsupponi necessum est) & videndum
quis sit numerus tangentis talis arcus, nimirum
212510. Distantia v. inter locum C, & fundamentum
altitudinis B, investiganda est catenâ,
funiculo, vel aliâ mensurâ, sitque ea 40 part erit
ergò per Regulâ proport. ut 100000. ad 212510;
ita 40. ad altitudinem quæsitam, quæ peractâ
operatione, erit 85. partium talium, qualium distantia
B C est 40.
Huic altitudini inventæ addendum est spatium illùd quod continetur inter centrum instrumenti & ipsam terram, si modo planum illus inter
(18)
C & B omninò sit Horizontale, quod quidem rarò contingit, ergò notandum est, ubi radius visivus, dioptram Horizonti parallelam transiens, tangat altitudinem propositam, pars ista, quæ infrà hunc locum continetur, mensuranda est, & altitudini per calculum inventæ addenda. Si verò radius iste visivus cadat infrà altitudinem, explorandum est quantum, & tantum ab altitudine inventa est tollendum.
Quantum autem infrà cadat sic explorari potest: juxtà instrum. ponatur baculus, vel aliud quid cui imprimatur nota, quæ sit in eadem altitudine cum centro instrumenti, baculo sic stante, elevatur instrument., donec per dictam dioptram conspiciatur imum altitudinis dimetiend instrumento in isto situ & loco quiescente, ponatur iterum in baculo nota, centro instrumenti directè respondens, spatium inter has notas in baculo contentum, ab inventa altitudine est detrahendum. Si verò radius prædictus multum cadat infrà vel suprà altitudinis fundamentum, tunc alio modo inquirenda est altitudo, de quo in problemalibus tertio & quarto dicetur.
Notandum & hoc est, si proposita altitudo fuerit pyramidalis, ut turres & ejusmodi res aliæ, tunc mensuranda est distantia, quæ est inter instrumentum & punctum illud, quod perpendiculariter subest Cuspidi altitudinis propositæ. Quando itaque illud punctum vel ignoratur, vel occultatur, tunc altitudo illa tutius & rectius per duas stationes metienda est, quod quomodò fiat, dicetur infrà Probl. 6.
(19)
Problema II.
Partem altitudinis accessibilis investigare.
ESto altitudo D F, cujus pars D E sit inquirenda.
In primis metior ab F versus G, distantiam
quemcunque v. g. 50. pert. in G colloco instrumentum
ad perpendiculum, & eodem modo,
quo in problemate præcedenti factum est, observo
 angulum F G D, qui sit
65.54'. ejus tangens est
220108. Dico itaque
ut 100000. ad 220108;
ita 50 ad altitudinem D
F, 110. Deinde observo
angulum F G E, sitque
ille 55.57'. Cujus
tangens est 147977.
Itaque ut 100000. ad
147977. ita 50. ad altitudinem
F E, 74 quâ
subtractâ de 110 relinquentur
36. pro altitudine
D E quæsita.
angulum F G D, qui sit
65.54'. ejus tangens est
220108. Dico itaque
ut 100000. ad 220108;
ita 50 ad altitudinem D
F, 110. Deinde observo
angulum F G E, sitque
ille 55.57'. Cujus
tangens est 147977.
Itaque ut 100000. ad
147977. ita 50. ad altitudinem
F E, 74 quâ
subtractâ de 110 relinquentur
36. pro altitudine
D E quæsita.
ALITER
Tangentem minoris anguli de tangente majoris subtraho, remanebit differentia tangentium, scil. 72121. Cum hac differentia ita procedo: ut 100000. ad dieffer. tang. 72121. ita 50. ad partem altitudinis quæsitam D E, factâ operatione, prodibunt 36. ut ante.
(20)
Problema III.
Altitudinem rei accessibilis per basim
sursum Vergentem explorare.
SIt altitudo H I, investiganda ex basi obliqua
K I quæ sit 36. partium. Instrum. ad perpendiculum
in K collocato, primò observo ang. I K L,
 qui sit 53.2'. deinde ang.
I K H, sitque 104.44'. quia
itaque angulus H I K, æqualis
est angulo I K L, per
29. I. Eucl. erit au(sic)ulus
I H K 22.14'. Cujus sinus
est 37838. Cum itaque
Ax. 2.
Pitisci.
Latera se habeant ad invicem
ut sinus angulorum ipsis
oppositorum. & contrà.
Dico: ut 37838 (sinus ang.
I H K, 22.14'.) ad latus I K
36. ita 96712. (sinus ang.
I K H) ad altitudiné quæsitam,
92.
qui sit 53.2'. deinde ang.
I K H, sitque 104.44'. quia
itaque angulus H I K, æqualis
est angulo I K L, per
29. I. Eucl. erit au(sic)ulus
I H K 22.14'. Cujus sinus
est 37838. Cum itaque
Ax. 2.
Pitisci.
Latera se habeant ad invicem
ut sinus angulorum ipsis
oppositorum. & contrà.
Dico: ut 37838 (sinus ang.
I H K, 22.14'.) ad latus I K
36. ita 96712. (sinus ang.
I K H) ad altitudiné quæsitam,
92.
Nota. quando occurrit angulus obtusus, ut in hoc exemplo I K H, tum semper sumendus est sinus complementi ejus ad semicirculum, quod hic semel monuisse sufficiat, & in sequentibus tenendum.
(21)
Problema IV.
Altitudinem rei accessibilis ex basi deorsum
Vergente metiri

POnatur altit. M N. dimetienda ex basi M obliqua N O. 38. pert. Instrumento in O ita collocato, ut per dioptram immobilem conspiciatur imum altitudinis, ut N. per mobilem v. ejus summum, M. notetur angulus N O M, qui sit 45.17'. Deinde collocetur instrumentum ad perpendiculum, ut habeatur angulus M O P, sit ille 25.2'. Dico ergò per axioma in antecedente problemate citatum, ut 42314 (sinus angul. M N O, 25.2'.) ad latus N O, 38. ita 71059 (sinus ang. N O M, 45.17'.) ad altit. N M, quæsitam, 64. ferè.
Problema V.
Partem altit. rei access. per basim obli-
quam inquirere.
SIt altit. R Q, cujus pars Q V investiganda proponitur. Sumo itaq; distantiam pro lubitu
(22)

R S sit illa 32 pert. & in S colloco instrumentum, observoque primum ang R S V, qui invétus sit 59.19'. Deinde ang. V S Q sitque ille 18.35'. tumq; ang. Q S T. 31.25'. Tribus his angulis collectis, & à semicirculo subtractis, relinquentur 70.51'. pro ang. V R S. Iam dico: ut 76417 (sin. ang. R V S, 49. 50'.) ad basim R S, 32; ita 94466. (sin. ang. V R S, 70.51'.) ad latus V S, 39. Rursus, ut 52125. (sinus ang. V Q S, 31.25'. est enim æqualis ang. Q S T,) ad latus V S, 39. ita 31592. (sinus ang. V S Q, 18.25'.) ad latus sive altitudinem V Q, quæsitam. 24.
Problema VI.
Altitudinem rei inaccessibilis per duas
stationes ex basi recta invenire.
ESto altit. A B, inccessibilis, cujus quantìtas ut innotescat, eligo duas stationes pro arbitrio, ita tamen, ut altitudo proposita & stationes assum-
(23)
ptæ sint in una linea recta, sintque istæ C & D, in
quarum alterutra, v. g. in C, colloco instrument.
ad perpend. & observo ang. A C B, quem invenio
63.26'. Deinde procedo rectà versus altitudinem,
usque in D, simulque distantiam C D me
 tior, quæ sit 20. pert. instrumento
ad perpendiculum
in D collocato,
observo ang. A D B, qui
sit 70.21'. quo de semicirculo
ablato, relinquitur
angulus B D C, 109.
39'. qui cum ang. D C B,
63.26'. facit 173.5'. quibus
de 180. sublatis, manebit
ang. D B C, 6.55'.
Cujus sinus 12042. se habet
ad 20. ut 89441. (sinus
ang. D C B, 63.26'.) ad
latus B D, 149. ferè.
Iam dico: ut 100000. ad
94176 (sinus ang. A D B
70.21'.) ita 149. ad altit.
quæsitam, 140.
tior, quæ sit 20. pert. instrumento
ad perpendiculum
in D collocato,
observo ang. A D B, qui
sit 70.21'. quo de semicirculo
ablato, relinquitur
angulus B D C, 109.
39'. qui cum ang. D C B,
63.26'. facit 173.5'. quibus
de 180. sublatis, manebit
ang. D B C, 6.55'.
Cujus sinus 12042. se habet
ad 20. ut 89441. (sinus
ang. D C B, 63.26'.) ad
latus B D, 149. ferè.
Iam dico: ut 100000. ad
94176 (sinus ang. A D B
70.21'.) ita 149. ad altit.
quæsitam, 140.
Brevius.
Cognitis angulis A D B & A C B, sumantur tangentes eorum complementorum ad 90. & minor à majore subtrahatur, ut habeatur differentia quæ in hoc exemplo erit 14297. Dico jam; ut, 14297. (diff. tang. compl.) ad 100000. ita 20. ad quæsitam altit. A B, 140. ut prius. Cui altitudo instrumenti est adiicienda.
(24)
Problema VII.
Partem altit. inaccessibilis investigare.
SIt altitudo E F, inaccessibilis, & quæretur ejus
pars G F. Electis duabus stationib. H & I, pono
instrum. in H. ad perpend. & observo angulos
E H G, 60.57' & E H F, 67.36'. quibus notatis
retrocedo ab H ad I, sitque ea distantia 30. pert. ex
I(sic)similiter observo ang. H I G, 45.49'. tum ang.
H I F, 54.11'. Datis jam angulis E H F, & E I F.
 dantut etiam
eorum complemēta,
quorum
tangentium
differentia
30949 ut
se habet ad
100000, ita 30
ad altitudinem
E F, 97. Deinde
quæratur
differentia tangentium
angulorum
E G I,
& E G H, qui
sunt complementa
angulorum
E I G &
E H G, eritque E
illa 41644. Dico ergò, ut 41644 ad 100000; ita
30. ad altitudinem E G 72. quâ ex altitudine E F,
97. detractâ, remanebit altitudo quæsita G F, 25.
dantut etiam
eorum complemēta,
quorum
tangentium
differentia
30949 ut
se habet ad
100000, ita 30
ad altitudinem
E F, 97. Deinde
quæratur
differentia tangentium
angulorum
E G I,
& E G H, qui
sunt complementa
angulorum
E I G &
E H G, eritque E
illa 41644. Dico ergò, ut 41644 ad 100000; ita
30. ad altitudinem E G 72. quâ ex altitudine E F,
97. detractâ, remanebit altitudo quæsita G F, 25.
(25)
Problema VIII.
Altit. inaccess. ex alia altitudine cognosere.
Casus I. ex altit. Minori.
SIt altit. K L inquirenda ex nota altitudine M N,
quæ sit 16. partium. INstrumento in N collocato,
oservo primò ang. M N K, qui sit 72.15'.
 De(sic)nde ang. K N L, sitque
ille 75.45'. Erit itata(sic)que
ut 100000. ad
328014 (secant. anguli
K N M, 72.15'.) ita 16.
ad latus K N. 52(?).
jam quia angulus L K
N, æquilis est ang. M
N K, erit ang. K L N,
32.0'. quare, ut ejus sinus
52991. ad 52(?) ita
96923. (sinus anguli K
N L, 75.45'.) ad altit.
quæsitam, 96.
De(sic)nde ang. K N L, sitque
ille 75.45'. Erit itata(sic)que
ut 100000. ad
328014 (secant. anguli
K N M, 72.15'.) ita 16.
ad latus K N. 52(?).
jam quia angulus L K
N, æquilis est ang. M
N K, erit ang. K L N,
32.0'. quare, ut ejus sinus
52991. ad 52(?) ita
96923. (sinus anguli K
N L, 75.45'.) ad altit.
quæsitam, 96.
Casus II. ex altit. majori.
Sit investiganda altit. O P, ex cognita altitudine Q R, quæ sit 86. partium. Ex loco R igitur observo angul. O R Q, qui inventus sit 20.10'. ang. v. P R O, sit 26.21'. Erit ergò, ut 100000. ad 115665. (sec. ang. O R Q, 30.10'.) ita 86. ad latus R O 99 Iam in triangulo P R O, dantur omnes au(sic)uli,
(26)

ang. enim P O R, æqualis est angulo O R Q) erit angulus O P R 123.29'. Cujus sinus (id est ejus compl. ad semicirculum( est 83404 quare , ut 83404. ad 99; ita 44385. (sinus ang. 26.21') ad altit quæsitam 53.
Problema IX.
Altitudinem in (sic)access. ex parte acclivi-
tatis montis metiri.
SIt investiganda alt. T S, ex obliquitare montis Z. Eligo ergo duas stationes pro lubitu, v. g. V & X, quarum distantia sit 30 pert. primum itaque colloco instrumentum in V, & observo ang. Y V T, 39.48'. item ang. T V S, 82.49'. nec non ang. S V X, 108.13'. Deinde confero me ad stationem secundam X, ubi ob(sic)ero ang. S X V, 49.28'. Hinc dico, ut 37972. (sinus ang. V S X, 22.19'.)
(27)
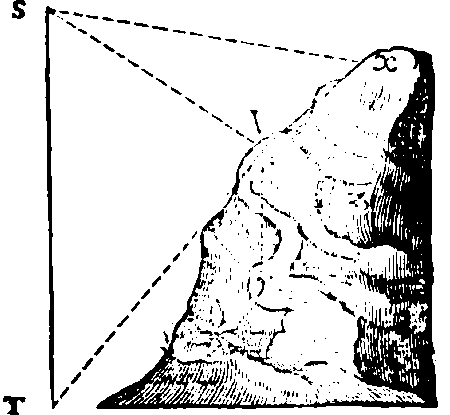
ad latus V X, 30; ita 76002. (sinus ang. S X V, 49.28'.) ad latus S V, 60. Deinde, ut 64010. (sinus ang. S V T, 82.49'.) ad altit. quæsitam T S, 93. ferè.
Problema X.
Altit. inac(sic)ess. in monte positam, ex alia
altitudine etiam in monte posita metiri.
SIt inquirenda altit. E D. ex altit. nota A B, 10. part. Primo ex B, observo ang. A B E, 71. 34'. & ang. A B D, 50.12'. Deinde ex A, ang. C A E, 80.32'. & ang. C A D, 56.19'. jam subtraho 80.32'. è semicirculo, rstat ang. B A E,
(28)
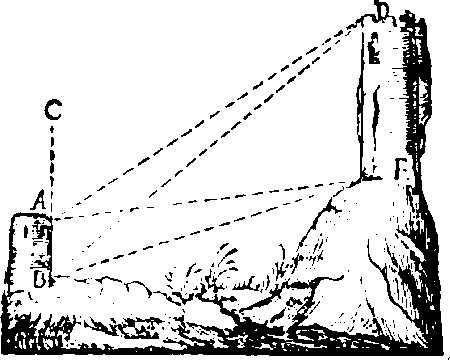
99.28'. erit itaque ang. A E B, 8.58'. Cujus sinus 15586. ut se habet ad A B 10. ita 94869. (sinus ang. A B E 71.34') ad latus A E, 61. Subtracto ang. C A D, 56.19'. ab ang. C A E, 80.32'. restat ang. D A E, 24.13'. ang. v. A D E, æqualis est ang. C A D, 56.19'. erit ergò, ut 83218. (sinus ang. A D E, 56.19'.) ad latus A E, 61, ita 41018. (sinus ang. D A E, 24.13'.) ad altit. quæsitam, 30.
Problema XI.
Altitudinem, cujus basis non videtur,
ex basi transversa metri.
SIt altitudo G F, inquirenda, cujus pars tantum suprà arbores vel alia impedimenta apparet, nec datur copia ad eam directè accedendi vel ab eadem recedendi, sed ad latus tantum secedendi. Itaque prout fert occasio, eligo duas stationes, H & I, & in I, pono baculum, cui signum aliquod (chartam, linteolum vel aliud quid) in ea altitudine af-
(29)
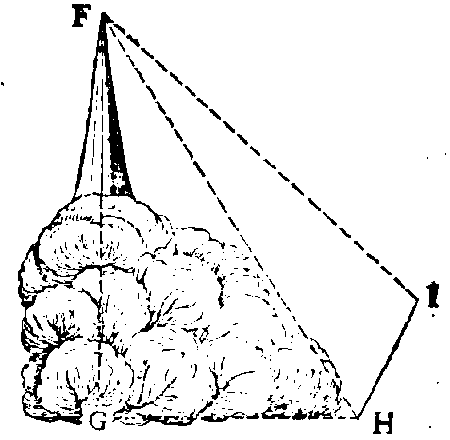
figo, ut respondeat centro instrumenti ibidem collocati. Hoc facto, instrumentum colloco in H, primò ad perpend. & observo ang. G H F, qui sit 57.27'. deinde instrumentum ita inclino ut per unam dioptram conspiciatur summitas altitudinis F, per alteram v. signum baculi in I positi, atque tunc noto ang. F H I, qui sit 60.8'. quo facto, instrument. transfero ad alteram Stationem I, baculo in H, relicto cum signo alîquo affixo, in tali altitudine, qualem centrum instrumenti in dicta inclinatione habebat. In I vicissim instrument. ita statuo, ut per alterutram dioptram F, per alteram v. signum baculi in H relicti conspiciatur, atque ita observo ang. F I H, 104.47'. Dist. v. inter H & I, sit 30 pert. Dico jam, t 26022. (sinus ang. H F I, 15.5'.) ad latus F H, 111. Porrò, ut 100000. ad 84292. (sinus ang. F H G, 57.27'.) ita latus F H, 111 ad G F. 94.
(30)
Problema XII.
Altitudinem metiri per basim transversam,
si basis ejus appareat.

SIt altit. L K, exploranda per basim transversam M N, colloco ergò instrument. in N primò ad perpend. & observo angulum L N K, 60.42'. deinde horizonti parallelum, & cōstituo angulum L N M, rectum quidem si ita ferat commoditas loci, alias obliquum, & tunc eum noto Posteà colloco instrum. in M, prallelôs ad horizontem, & observo ang. L M N, qui sit 61.24'. Distantia M N, sit 30. pert, itaque ut 100000 ad 84292. (sinus ang. F H G, 57.27'.) ita 30. ad L N, 55. ulterius, ut 10000. ad 178197. (tang. ang. L N K, 60.42'.) ita 55 ad L K, alt. suprà instrum. 98.
(31)
Problema XIII
Longitudinem alicujus rei rectilineæ inve-
nire, Cujus pars tantum suprà aliam alti-
tudinem eminet.
SIt inquirenda longitudo Q O. Cujus pars P O,
eminet suprà altitud. R P. Primum in venire
 oportet punctū S, quod perpendiculariter subsit extremitati
O, quod facile fieri potest perpendiculo
è manu suspendo & versus O ad latus directo. Deinde
in linea R S continuata pono instrumentum
ubicunq; placuerit, ut in T, & observo ang. P T R,
59.16'. tum ang. O T R 71.57'. sitq; distantia
R S, 7. & S T 15. part. Dico ergo; ut 100000.
oportet punctū S, quod perpendiculariter subsit extremitati
O, quod facile fieri potest perpendiculo
è manu suspendo & versus O ad latus directo. Deinde
in linea R S continuata pono instrumentum
ubicunq; placuerit, ut in T, & observo ang. P T R,
59.16'. tum ang. O T R 71.57'. sitq; distantia
R S, 7. & S T 15. part. Dico ergo; ut 100000.
(32)
ad 306857. (tang. ang. S T O, 71.57'.) ita 15. ad S O, 46. Deinde, ut 100000. ad 168196. (tang. ang. P T R, 59.16'.) ita R T, 22. ad R P, 37. quâ subtractâ de S O 46. restabunt 9. pro V O. Erit itaque ut O V 9. ad V P 7. ita O S, 46. ad S Q, 35 (?), cujus quadratum si addatur quadrato è 46. & inde extrahatur radix, habebitur longitudo Q O, 58. quam proximè.
Aliter
Potest hoc etiam alia via perfici. scil. per duas stationes, quæ sint T Z, quarum distantia sit 10. partium. Observatis ex Z angulis P Z R, 49.9'. & O S, juxta 6. vel 7. probl. His cognitis, & pro Radio sumptis, facile inveniuntut R T, & S T, quarum minore ex majori subtractâ, manet R S, item P R de O S, manebit O V, quibus datis, procedendum ut modo dictum est.
(33)
Problema XIV.
Altitudinem montis ex altit. turrū in
eo posita invenire.
SIt altitudo montis Y Z investiganda ex altitudine
cognita Y X, quæ sit 24. part. Primò
quæro signum aliquod ad montis pedem, quod sit
in A, deinde instrumento, ad perpendiculum collocato,
observo ang. A Y Z. qui sit 60.57'. similiter
in X ang. A X Z, 50.34'. erit ang. X A Y, 10.
23'. ut itaque ejus sinus 18023. ad X Y 24 ; ita
 772. (sinus ang. A X Z, 50.34') ad latus A Y,
103. quo cognito, dico ut 100000. ad 48457.
(sinum compl. ang. A Y Z, 60.47'.) ita 103. ad altitudinem
quæsitam 50.
772. (sinus ang. A X Z, 50.34') ad latus A Y,
103. quo cognito, dico ut 100000. ad 48457.
(sinum compl. ang. A Y Z, 60.47'.) ita 103. ad altitudinem
quæsitam 50.
(34)
Vel sic.
Ut 26732. (differentia tangentium angulorum X A Z, & Y A Z) ad 55506. (tangentem minorem) ita 24. ad altitudinem quæsitam 50. ut ante.
Problema XV.
Altitudinem turris ax alia turri in eadem
montis obliquitate posita deprehendere.
SIt altitudo C B, inquirenda ex data altitudine
D E 25. part Instr. in E ad perpend. collocato,
observo ang. C E D, qui sit, 128.2'. deinde
ex D, ang. C D E, 36.57'. & ang. B D C, 34.40'.
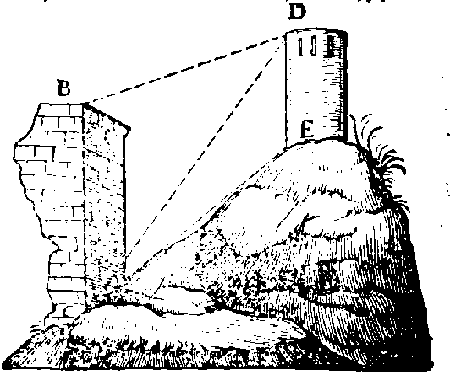 tum dico : ut 25910. (sin. ang. D C E, 15.1') ad
25 : ita 78765 (sin. ang. C E D, 128.2'.) ad latus
C D, 76. In triangulo itaq; B C D datum est
tum dico : ut 25910. (sin. ang. D C E, 15.1') ad
25 : ita 78765 (sin. ang. C E D, 128.2'.) ad latus
C D, 76. In triangulo itaq; B C D datum est
(35)
unum latus, & omnes anguli, nam ang. B C D, æqualis est ang. C D E, ideoque tertius C B D ignotari non potest. ut ergò 94896. (sinus ang. C B D.) ad latus C D 76 ; ita 56880 (sinus ang. B D C, 34. 40'.) ad C B 46. quæ erat inquirenda.
Problema XVI.
Altitudinem montis ex distantia aliqua
in vertice montis data, investigare.
SIt e.g. mons HFG, tàm præruptus ut nec
ascendere, nec descendere liceat, jubetur nihi-
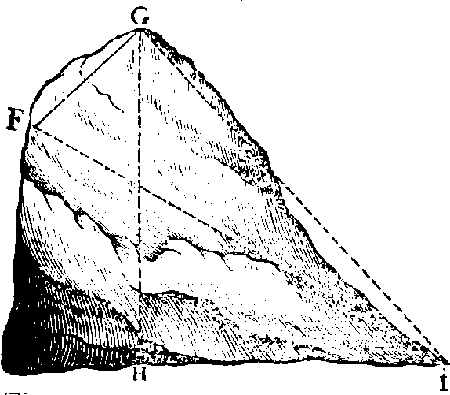 lominus, ut ejus altitudo inquiratur. Primum itaque
quæratur signum aliquod in imo montis pede
lominus, ut ejus altitudo inquiratur. Primum itaque
quæratur signum aliquod in imo montis pede
(36)
situm, quod sit in I, deinde eligantur duæ stationes ita ut ex utraque signum I commode videri possit, ut in G & F, in F ponatur baculus, inque eo signum aliquod ad altitudinem instrumenti non aliter ac in probl. XI, dictum est, instrumentum v. collocetur ad perpend. in G, & observetur ang. H G I, qui sit 43.37'. deinde ita inclinandum est instrum. ut per alterutrā dioptram conspiciatur I, per alteram v. signum baculi in F positi, & notetur angulus F G I, qui in hoc exemplo ponitur rectus. Deinde relicto in G baculo cum signo ad altit. instrumenti imposito, collocetur instrumentum in F & dirigatur ita, ut per alteram signum baculi in G, & notetur angulus G F I, sitque 72.31'. Distantia inter F & G, sit 40. Primò itaque inquiratur latus G I sic : ut 100000. ad 317481. (tang. ang. G F I, 72.31'.) ita 40 ad latus G I, 127. Hinc, ut 100000. ad 72397. (sinum compl. ang. H G I 43. 37'.) ita 127. ad H G alt. quæsitam, 92. ferè.
Quod si ang. I G F non fuerit rectus, operandum erit, juxta axio. 2. Pitisci, suprà probl. tertio citatum, ut multoties in præcedentibus factum est.
DE DISTANTIIS,
Problema XVII.
Distantiam duorum locorum invenire.
SIt distantia M K invenienda, quod fieri oportet per duas stationes, ut M & L, in quarum alterutra, ut in M, collocetur instrumentum parallelôs ad planum horizontis, & moveantur ita dioptræ,
(37)

ut per unam conspiciatur K, per alteram baculus in futura statione L erectus, noteturque angulus K M L, qui sit 75.19'. transferatur deinde instrum. in L, & observetur ang KLM, sit ille 82.50' distantia v. L M, mensurâ quâdam est inquirenda, sit ea v. g. 30. part. erit ergò ut 37217. (sinus ang. M K L, 21. 51'.) ad latus L M, 30 ; ita 99218 (sinus ang. K L M, 82.50'.) ad distantiam quæsitam, 80.
Plerunq; tamen, si modo nulla adsint impedimenta, unus angulorum constituitur rectus ob faciliorem operationem.
Problema XVIII.
Distantias plurium locorum in eadem
linea recta dispositorum invenire.
SInt diversa loca N, P, Q, R, S, in una recta linea sita, quorum distantiæ quæruntur. Colloco igitur instrumentum in O ita ut ang. O N S sit
(38)

rectus, si fieri potest ut facilior sit operatio, & omnes angulos ordine observo, e.g. N O S, 70 43'. N O R, 64.59'. N O Q, 59.45' & N O P, 50: 51'. Distantia O N, sit 35. pert. quibus cognitis dico: ut 100000, ad 285821. (tang. ang. N O S, 70.43') ita 35, ad distantiam N S, 100. Deinde, ut 100000. ad 214288. (tang. ang. N O R, 64. 59'.) ita 35. ad dist. N R, 75. quâ è 100. subtractâ, remanet dist. R S, 25. Porro, ut Radius 100000. ad 171472. (tang. ang. N O Q, 59.45') ita 35. ad N Q, 60, quâ detracta è distantia N R 75. remanebit dist. Q R, 15. Postremò, ut 100000. ad 122830. (tang. ang. N O P, 50.51') ita 35. ad N P, 43. quæ si subtrahatur à 60. manebit dist, P Q, 17. pert.
Vel si mavis
Juxta posteriorem modum probl. secundi per differentias tangentium operari, eòdem res redibit. e.g. ut 100000. ad 71533. (diff. tang. angulorum N O S & N O R,) ita35. ad dist. R S, 25. ut prius. Et sic in cæteris.
(39)
Problema XIX.
Distantiam duorum locorum ex basi
transversa reperire.
POnatur distantia T V, inquirenda ex basi transversa
X Z, 60 pert. Angulis in utraque statione
observaris nempe T X V 97.10'. V X Z. 43.
32'. item T Z V. 75.32' & T Z X, 24.45'. Anquli
X T Z, & X V Z latere non possunt, dico itaque,
ut 25122. (sin. ang. X T Z, 14.33'.) ad 60 ;
ita 41866. (sin. ang. X Z T, 14.45'.) ad latus X T,
 100. Deinde ut 59037. (sin. ang. X V Z, 36.11'.
ad 6(?): ita 98393. (sin. ang. X Z V, 100.17') ad
latus X V, 100. Quia itaque latera T X, X V,
sunt æqualia, erunt anguli X T V, & X V T, æquales,
per 5. 1. Eucl. subtraho igitur 97.10'. è
180. residuum erit 82.50'. cujus dimidium 41.
25'. pro ang. X T V, vel X V T, ut ergò, 66153.
(sin. ang. X T V, 41.25') ad 100. ita 69218.
(sin. ang. T X V, 97.10') ad distantiam quæsitam
T V, 150.
100. Deinde ut 59037. (sin. ang. X V Z, 36.11'.
ad 6(?): ita 98393. (sin. ang. X Z V, 100.17') ad
latus X V, 100. Quia itaque latera T X, X V,
sunt æqualia, erunt anguli X T V, & X V T, æquales,
per 5. 1. Eucl. subtraho igitur 97.10'. è
180. residuum erit 82.50'. cujus dimidium 41.
25'. pro ang. X T V, vel X V T, ut ergò, 66153.
(sin. ang. X T V, 41.25') ad 100. ita 69218.
(sin. ang. T X V, 97.10') ad distantiam quæsitam
T V, 150.
Quod autem latera T X (?) X V, inventa sint hic æqualia, id per accidens factum est, cum v. inæqualia, fuerint, quomodo tunc anguli ipsis oppositi sint inveniendi, dicetur probl. sequenti.
(40)
Problema XX.
Distantiam duorum locorum ex basi re-
trocadente inquirere.
SIt distantia A B indaganda ex basi D C 26. pert.
Instrumento in C collocato, & baculo quodam
in D, observo ang. A C B, 118.30'. B C D, 124.0'.
 D C A, 117.30'. deinde colloco instrumentum
in D. baculo in C relicto, & observo ang. C D A,
46.47'. item angulum C D B, 39.52'. Iam dico :
ut 27088. (sinus ang. D A B, 15.43'.) ad 26 ; ita
72876. (sinus ang. C D A, 46.47'). ad latus C A,
70. Sic in altero triangulo, ut 27787. (sinus ang.
C B D, 16.8'.) ad 26 ; ita 64100. (sinus ang.
C D B, 39.52'.) ad latus C B, 60. Quia autem
in triangulo A C B, dantur duo latera, & angulus
D C A, 117.30'. deinde colloco instrumentum
in D. baculo in C relicto, & observo ang. C D A,
46.47'. item angulum C D B, 39.52'. Iam dico :
ut 27088. (sinus ang. D A B, 15.43'.) ad 26 ; ita
72876. (sinus ang. C D A, 46.47'). ad latus C A,
70. Sic in altero triangulo, ut 27787. (sinus ang.
C B D, 16.8'.) ad 26 ; ita 64100. (sinus ang.
C D B, 39.52'.) ad latus C B, 60. Quia autem
in triangulo A C B, dantur duo latera, & angulus
(41)
ab eis comprehensus, erit juxta tertium ax. Pit. Vt summa duorum laterum add differēi(sic)iam eorundem, ita tangens simidii summæ duorum angulorum ipsis oppositorum, ad tangentem infrà vel suprà dimidium. Exemplum ergò sic stabit: ut 130. summa laterum, ad 10. diff. eorum ; ita 59493. tang. dimidii summæ angulorum opp. ad 4576. tang arcus 2.37'. qui si addatur ad dimidium summæ angulorum, scil. 30.45'. erit totus 33.22'. pro ang. A B C idem ab eodem dimidio subtractus relinquet 28.8'. pro ang. B A C. Iam dico : ut 47152. (sinus ang. C A B, 28.9') ad latus C B 60 ; ita 87881. (sinus ang. A C B, 118.30'. ( ad distantiam A B quæsitam 112. ferè.
Problema XXI.
Distantiam duorum locorum inquirere
si dantur libera stationes.
SIt inquirenda distantia E F, Primò pono instrumentum
in G & observo ang. E G F, qui
 sit 94.0'. Et quia facilius resolvuntur triangula,
sit 94.0'. Et quia facilius resolvuntur triangula,
(42)
rectangula quâm obliquangula, ideo constituo ab utraque parte ang. rectum, ut E G I, & F G H, deinde sumo à G versus H & I distantias pro lubitu, æquales vel inæquales, sint in hoc exemplo æquales, quælibet 20 pert. Et observo ang. G I E, 71. 34'. & ang. G H F, 66.30'. dico ergò, ut 100000. ad 300028 (tang. ang. E I G. 71.34') ita 20. ad latus E G 60. Sic ab altera parte : ut 100000. ad G F, 46. quo facto inquiro per axioma præcedente probl. citatum, angulos G E F, & G F E, eritque ang. G EF, 35.59'. ang. v. G F E, 50.1' quarè sic dico : ut 76623. (sin. ang. G F E, 50.1'.) ad 60 ; ita 99756. (sin. ang. E G F, 94.0'.) ad latus E F, quæsitum. 78.
Problema XXII.
Distantiam duorum vel plurium locorum
in linea recta invenire, si prima statio in eo-
rum linea datur, & ab ea ad angulos
rectos recedere licet.
VT sint loca L, P, O, N, M, K in eadem linea
posita, quorum distantiæ sunt inquirendæ. Su
 matur ergò in ea linea punctum aliquod ut N, ad
quod constituantur anguli recti Q N O & Q N M,
matur ergò in ea linea punctum aliquod ut N, ad
quod constituantur anguli recti Q N O & Q N M,
(43)
ponaturque instrumentum in Q & observuntur ang. N Q L, 62.44'. N Q P, 54.28'. N Q O, 30.58'. N Q M, 31.37'. N Q K, 53.16'. quibus cognitis, & distantia Q N, 50. erit ut 100000. ad 194023. (tang. ang. N Q L, 62 44'.) ita 50. ad dist. N L 97.
Porrò, ut 100000. ad 140022 (tang. ang. N Q P, 54.28'.) ita 50. ad dist. N P. 70. quâ ex priori subtractâ, restabunt 27 pro dist L P. Et sic in reliquis omnibus est pro cedendum. Si v. quis maluerit per differentias tangentium operari, ut problemate 2. & aliis indigitarum est, licebit.
Suorum tantum locorum distantia desideretur, verbi gr. inter L & K, potest id unicâ operatione absolvi, si addantur tangentes angulorum L Q N, & N Q K, & dicatur ; ut 100000 ; ad 328020. sum. tang. ita 50. ad dist. L K 1 64. Et sic in cæteris.
Problema XXIII.
Idem ex basi obliqua prestare.
SInt distantiæ R X, X Y, Y T, T S, indagandæ ex
basi obliqua T V, sitq; ea 75. pert. Primò ob-
 serventur ang. R T V, 63.5'. & S T V, 136.55'.
ponatur deinde instr. in V, ibiq; observentur ang.
serventur ang. R T V, 63.5'. & S T V, 136.55'.
ponatur deinde instr. in V, ibiq; observentur ang.
(44)
T V R, 71.34'. T V X, 48.12'. T V Y, 23.32'. T V S, 24.32'. Iam per 2. ax. ut 71141. (sinus ang. V R T, 45.21'.) ad 75. ita 94869. (sinus ang. R V T, 71.34'.) ad latus R T 100. Item, ut 93179. (sinus anguli V X T, 68.43') ad 75. ita 74547 (sinus ang. X V T, 48.12') ad latus X T, 60. quibus è 100. subductis restabunt 40. pro distantia R K. atque ita porrò in reliquis.
Problema XXIV.
Dist. Navis ab aggere explorare.
SIt agger vel murus K I, & in mari sit navis in L,
quæratur quantum illa distet à muro K I. Ponatur
instrumentum in I ad perpendiculum &
 observetur ang. K I L qui sit 76.31'. sitq altitudo
muri 30. part. erit ergò ut 100000. ad 417064.
(sin. ang. K I L, 76.31'.) ita 30. ad distantiam
quæsitam 125.
observetur ang. K I L qui sit 76.31'. sitq altitudo
muri 30. part. erit ergò ut 100000. ad 417064.
(sin. ang. K I L, 76.31'.) ita 30. ad distantiam
quæsitam 125.
Problema XXV.
Dist. navium à se invicem experiri.
SInt duæ naves N & O, quarum à se invicem distantia quæritur? Ponatur ergò instrumen-
(45)
tum ad perpen. in superiori parte mali, ut in M,
& observetur ang. N M O, qui inventus sit 89.30'.
 malus v. ab M, usque ad aquam, sit 4. pert. itaque
ut 100000. ad 11458865. (tang. ang. N M O,
89.30'.) ita 4. ad dist. quæsitam 458. pert.
malus v. ab M, usque ad aquam, sit 4. pert. itaque
ut 100000. ad 11458865. (tang. ang. N M O,
89.30'.) ita 4. ad dist. quæsitam 458. pert.
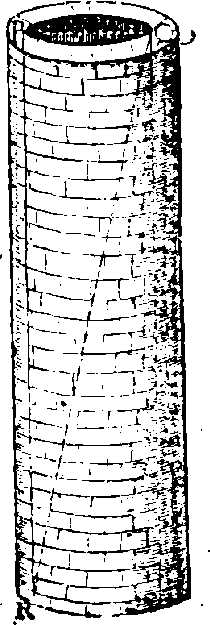
Pobl. XXVI.
Profunditatem putei
notam reddere.
SIt Puteus R P Q, cujus profunditas, usque ad aquam sit in vestiganda. Collocetur instrumentum in Q, ad perpend. & dirigatur dioptra mobilis donec per eam conspiciatur punctum contactus aquæ & parietis, in R, & notetur ang. R Q P, qui sit 77.21'. putei v. latitudo P Q sit 22. ped. erit ut 100000, ad 445547. (tang ang. 77.21'.) ita 22. ad profunditatem suprâ aquam, 98. pedum.
(46)
Problema XXVII.
Tractum lineæ rectæ per varia impedimen-
ta transeuntis, datis duobus punctis, invenire.
SIt linea recta A B, transiens per impedimenta
D, E, F, Cujus quidem extrema dantur scil. A
& B, sed quæritur ubinam illa inter hæc impedimenta
transeat ? Ponatur ergò instrumentum ubi
visum fuerit, v. g. in C, & observetur ang A C B,
 qui sit 108.12'. Inter hæc impedimenta erigantur
baculi ; ut in G & H, & instrumento notentur anguli,
A C G, 15.6' G C H, 34.23'. H C B, 58.
43'. Et catenâ vel fuuiculo mensurentur A C &
C B, sitque A C, 80. B C v. 40. pert. erit ergò per
axio. 3.probl, 20. citatum, ang. C A B, 22.20'.
& ang. C B A, 49.28'.itaque ut 60783. (sinus
ang. A G C, 142.34'.) ad A C, 80 : ita 37999 (sin.
ang. C A G, 22.20'.) ad latus C G, 50. in linea
ergò C G, mensurentur istæ 50. perticæ, & in termino
mensurationis, ut in G ponatur instrument.
& dioptra mobilis ad talem angulum qaulis est,
A G C, qui angul. notus est, cum noti sint anguli
C A G & A C G, angulo isto in instrumento
constituto, moveatur instrumentum donec per al-
qui sit 108.12'. Inter hæc impedimenta erigantur
baculi ; ut in G & H, & instrumento notentur anguli,
A C G, 15.6' G C H, 34.23'. H C B, 58.
43'. Et catenâ vel fuuiculo mensurentur A C &
C B, sitque A C, 80. B C v. 40. pert. erit ergò per
axio. 3.probl, 20. citatum, ang. C A B, 22.20'.
& ang. C B A, 49.28'.itaque ut 60783. (sinus
ang. A G C, 142.34'.) ad A C, 80 : ita 37999 (sin.
ang. C A G, 22.20'.) ad latus C G, 50. in linea
ergò C G, mensurentur istæ 50. perticæ, & in termino
mensurationis, ut in G ponatur instrument.
& dioptra mobilis ad talem angulum qaulis est,
A G C, qui angul. notus est, cum noti sint anguli
C A G & A C G, angulo isto in instrumento
constituto, moveatur instrumentum donec per al-
(47)
terutram dioptram conspiciatur signum in C relictum, tunc altera dioptra dabit tractum lineæ inter duo ista impedimenta. Eodem modo inquirenda est linea C H, quâ inventâ, & catenâ determinatâ, instrumentoque in ejus termino ut in H collocato, & dioptrâ mobili ad debitum angulum constitutâ, habebitur & ibi tractus quæsitus lineæ datæ.
Problema XXVIII.
Figuras rectilineas ex Charta in Campum
transferre.
SIt figura I K L M N O, in campum transferenda.
Primum itaque transportatore investi-
 gandi sunt omnes anguli, omnesq; lineæ mensurâ
quâdam sunt determinendæ. ut in hox exemplo sit
angulus OIK, 117.50'. I K L, 126.48'. K L M,
98.12' L M N, 120.8'. M N O, 114.48' N O I,
142.14'. lineæ v. I K, 46. pert. 1. ped. K L, 61.
gandi sunt omnes anguli, omnesq; lineæ mensurâ
quâdam sunt determinendæ. ut in hox exemplo sit
angulus OIK, 117.50'. I K L, 126.48'. K L M,
98.12' L M N, 120.8'. M N O, 114.48' N O I,
142.14'. lineæ v. I K, 46. pert. 1. ped. K L, 61.
(48)
pert. 9. ped. L M, 35.8. M N, 66.6. N O. 34. 8. O I, 27.4. quibus notatis praxis est instituenda. Si sit jam aliquis angulus in figura, quem in certum aliquod punctum in planitie cadere quis voluerit, tunc ab isto angulo est incipiendum, sit hoc verbi gratia in O, ergò in O erigendus est baculus, & ab O versus I, tot mensurandæ sunt partes, quot notatæ sunt in linea O I, ut in hoc exemplo 27. pert. 4. ped. idque juxta eum tractum ubi illam lineam O I, transire voluerit, in termino mensurationis ponatur instrumentum, in eoque constituatur angulus in Charta notatus, ut hic 117.50'. & dirigatur ita ut per unam dioptram videatur baculus in O, & ab altera parte ponatur baculus alius, ita ut is per dioptram alteram conspiciatur, versus quem ab instrumento mensurentur partes in Charta notatæ, sc. 45. pert. cum 1. ped. ab I, usq; in K, ubi iterum ponendum est instrumentum, baculo erlicto in I. Atque sic pergendum per totam circumferentiam. Cum tandem perventum fuerit ad N, collocetur ibi instrumentum, & moveatur circulus ut per unam dioptram videatur baculus relictus in M, per alteram v. baculus in O : si tunc angulus in instrumento convenerit cum angulo in charta notato, & distantia inter N & O, in plano catenâ mensurata, cum partibus in charta notatis, tunc rectè in campum translata est figura, sin minus ; error est commissus, & de novo instituenda est operatio.
(49)
Problema XXIX.
Vrbes & Fortalitia è campo in Chartam
delineare.
SIt urbs quædam cujus ambitus sit A B C D E F G H, quam in Charta delineare oportet.

Erectis in omnibus angulis hastis vel baculis, incipio ab aliquo angulo pro arbitrio v. g. ab angulo A, ubi instrum. colloco, & observo angulū H A B, qui sit 63.27'. deinde transfero instrum. in B, & simul lineam A B, Catenâ mensuro, quæ sit 35. pert. 5. ped. angulo A B C, observato (scil. 149.25'.) transfero instrumentum in C, & lineam B C catenâ invenio 48. pert. 4. ped. atque sic continuandum per totum circuitum, usque ad A, ubi inceptum erat.
Si quis scire desiderat, num omnes angulos ritè observaverit, nec ne : faciat ut sequitur : Primò addantur omnes anguli observati in unam summam, deinde multiplicentur 180. per numerum,
(50)
numero laterum binario minorem, factus ex hac multiplicatione, si æqualis fuerit summæ angulorum, rectè operatus est, sin minus ; non. Vt in figura prob. pæcedentis, ubi observati sunt anguli,
| O I K, | 117.50'. |
| I K L, | 126.48'. |
| K L M, | 98.12'. |
| L M N, | 120. 8'. |
| M N O, | 114.48'. |
| N O I, | 142.14'. |
| Summa, 720.0'. | |
Quia igitur in hac figura latera sunt 6. ideò multip. 180 per 4. (numerum scilicet binario minorem, quàm est numerus laterum 6) producetur numerus priori summæ æqualis, 720.
Cum verò etiam fuerint anguli externi, tunc subtrahantur sigillatim à 180. & residua addantur ab angulos internos, & postea addantur omnes in unam summam, deinde multipl. ut ante, 180. per numerum, numero laterum 2. minorem. Ubi notandum, quod semper duo latera, quæ angulum externum comprehendunt, sumenda sint pro uno. Sit exem. figura A B C D &c. in qua observati sint anguli:
| A B C | 49.25'. |
| B C D | 125.54'. |
| C D E | 119.24'. |
| D E F | 124.45'. |
| E F G | 133.50'. |
| F G H | 82.12'. |
| externus G H A | 79.6'. ejus compl. 100.54'. |
| H A B | 63.27'. |
| Summa, 900.0'. | |
Quia latera figuræ sunt 7. ideò multiplico 180. per 5. productus erit 900. qui quia æqualis est summæ angulorum, rectè observati sunt anguli.
Idemprocendi modus est in Fortalitiis delineandis, quæ si regularia fuerint, sufficit metiri 3. li-
(51)

neas ; scil. O P, Cortinam, P Q, alam, & Q R, faciem. Item duos angulos scil. ang. faciei & alæ P Q R, & ang. propugnaculi Q R S. Si verò irregularia fuerint, isto compendio uti non licet, sed per totum perimetrum, omnes lineæ & anguli sunt investigandi, & deinde beneficio transportatoris, & lineæ in æquales partes divisæ, in Chartam transferendi.
Problema XXX.
Mappas Topographicas conficere.
SIt e.g. tabula quædam construenda quæ contineat 9. pagos, literis A B C D E F G H I notatos. Eligo ergò duas stationes pro lubitu, ut in
(52)
I & H, & instrumentum ita in I colloco, ut per
diopraro immobilem, conspiciatur signum aliquod
in H, instrumento in hoc situ stante, facio
collimationes per dioptram mobilem ad omnes
 pagos sigillatim, notando angulos. v. g. H I G,
12 26'. H I F, 21.4(?)' H I E, 29.0' H I C, 41.
20'. H I D, 51.19' H I B, 86 25'. H I A, 112.
52'. quibus notatis, confero me ad alteram stationem,
H, & dist. inter I & H passibus vel aliâ mensurâ
notam mihi facio Et instrumento in H collocato,
ut per dioptram immobilem semper videatur
signum aliquod in priori statione I, altera
dioptra dabit angulos, scil. I H A, 19.52' I H D,
18.12'. I H F, 2(?).34'. I H B, 34.46'. I H C,
49.16'. I H E, 75. I H G, 30'. 98.2'. quibus cognitis,
facile in papyrum adminiculo transportatoris
Pagi transferri possunt, ut quilibet suum habeat
locum.
pagos sigillatim, notando angulos. v. g. H I G,
12 26'. H I F, 21.4(?)' H I E, 29.0' H I C, 41.
20'. H I D, 51.19' H I B, 86 25'. H I A, 112.
52'. quibus notatis, confero me ad alteram stationem,
H, & dist. inter I & H passibus vel aliâ mensurâ
notam mihi facio Et instrumento in H collocato,
ut per dioptram immobilem semper videatur
signum aliquod in priori statione I, altera
dioptra dabit angulos, scil. I H A, 19.52' I H D,
18.12'. I H F, 2(?).34'. I H B, 34.46'. I H C,
49.16'. I H E, 75. I H G, 30'. 98.2'. quibus cognitis,
facile in papyrum adminiculo transportatoris
Pagi transferri possunt, ut quilibet suum habeat
locum.
(53)
Problema XXXI.
Altitudinem Lapsus aquarum experiri.
SIt aqua vel Lacus quidam in X, & alius lacus
in K, quæritur quantum hic lacus suprà lacum
in X jaceat ? pono ergò instrumentum ad perp. in
M, ita(sic)ut aliquantulum suprà aquam elevatum sit,
& baculo L K ita collocato, ut inferiore suâ
 extremitate aquam tangat, dioptram horizonti parallelam
inspiciens, video ubi radius visivus in baculum
incidat, ut in V, ubi notam imprimi facio.
Hoc facto, baculum transferri jubeo in N, & iterum
video ubi radius visivus per dioptram transiens,
tangat baculum istum, ut in O, ubi etiam
ponenda est nota. jam mensurandum est illud spatium,
quod inter has n(?)tas comprehenditur, sit
illud v. g 9. pedum, & 4 dig. idque servandum.
Deleantur jam ambæ ista notæ, & baculo adhuc
in N quiescente, instrumentum tt(sic)ansfero in P.
ubi similiter observo punctum in baculo, in quod
linea per dioptram transiens ceciderit : ut in R, quo
extremitate aquam tangat, dioptram horizonti parallelam
inspiciens, video ubi radius visivus in baculum
incidat, ut in V, ubi notam imprimi facio.
Hoc facto, baculum transferri jubeo in N, & iterum
video ubi radius visivus per dioptram transiens,
tangat baculum istum, ut in O, ubi etiam
ponenda est nota. jam mensurandum est illud spatium,
quod inter has n(?)tas comprehenditur, sit
illud v. g 9. pedum, & 4 dig. idque servandum.
Deleantur jam ambæ ista notæ, & baculo adhuc
in N quiescente, instrumentum tt(sic)ansfero in P.
ubi similiter observo punctum in baculo, in quod
linea per dioptram transiens ceciderit : ut in R, quo
(54)
notato, transsfertur baculus in X, ibique ita collocatur, ut extremitate sua tangat ssuperficiē aquæ, & ubi linea per dioptram transienss, eum tangit, ut in T, ponenda est nota, spatium inter ambas notas contentum sit e.g. 7. ped. 3. dig. qui prioribus additi faciunt, 16. ped. & 7. dig. & tanta est altitudo lacus K, supra X, quæ erat inquirenda.
Hæc sunto ita breviter dicta de Astrolabii usu, qui plura desiderat, videat M. Dan. Swenterum, Arduiserum, Clavium, Faulhaberum, Ian Pietersen Dou, Maroloem, Stevinum, Metium, Witte-Kindum, Pitiscum, & alios, qui hac de re scripserunt.
(55)

PARS ALTERA
DE
QVADRANTE
ASTRONOMICO,
Membrum II.
De ejus Structura
Cap. I.
De Turricula.
 uamvis hoc Astrolabio, cujus
fabricam & usum jam dedi, Geometriæ
studiosis quodammodò satisfactum
esse confidam, studio tamen
Astronomiæ deditis, illud sufficere
non potest, quippe qui minutis primis non contenti,
minuta etiam secunda quoad fieri potest, sectantur.
Itaque ne ipsis prorsus defuisse videar,
brevem etiam, dilucidam tamen ut spero, manuductionem
tradere conabor de modo fabricandi
instrumentum Astronomicum, quo non solum
uamvis hoc Astrolabio, cujus
fabricam & usum jam dedi, Geometriæ
studiosis quodammodò satisfactum
esse confidam, studio tamen
Astronomiæ deditis, illud sufficere
non potest, quippe qui minutis primis non contenti,
minuta etiam secunda quoad fieri potest, sectantur.
Itaque ne ipsis prorsus defuisse videar,
brevem etiam, dilucidam tamen ut spero, manuductionem
tradere conabor de modo fabricandi
instrumentum Astronomicum, quo non solum
(56)
prima, sed etiam minuta secunda haberi possint.
Varia quidem sunt genera instrumentorum Astronom. ut Semicirculi, Quadrantes, Sextantes, Octantes, Sphæræ armillares, & id genus alia, Quadrantis verò structuram hic describere animus est, quam qui bene intellexerit, nullo negotio se in reliquorum structura expediet. Neque hic intelligendus est parvus aliquis Quadrans ab uno in alium locum portatilis, sed majoris alicujus quantitatis, cujus radius sit 3, 4 vel ultrà, pedum, qui semper in loco sibi destinato maneat, v. g. in Turricula quadam, quæ in sublimi & edito loco in hanc rem ædificata sit. Si eadem lateratia fuerit, eò melior & aptior erit ; tunc enim instrumento semel accuratè ad perpendiculum collocato, eum situm semper postea retinebit. Si v. lignea fuerit, multis detrimentis & variationibus obnoxia erit, ideoque observator certus esse non potest, an instrumentum debitum suum situm retineat, nec ne, unde cogetur semper instrumentum examinare, & ad pristinum situm redigere, si eundem amiserit. Cum v. Instrumentum seu Quadrans, ad perpendiculum in eo situ & loco, quem postea retenturus erit, sit collocatus, superiore suo latere (quod scil. horizonti parallelum est) suprà murum turriculæ aliquantulum supere minere debet, ut omnia sydera liberè absque omni impedimento, etiam circa horizontem observari possint. Deinde instrumentum unà cum turricula, tecto ex afferibus facto, tegi oportet, quod oblongas habebit fenestras, etiam ex afferculis factas, quibus apertis omnia cœli puncta, ab horizonte, usque ad Zenit observari queant. Tectum autem non immediat è muro, sed circulo cuidam ligneo, ex solida &
(57)
constanti materia constructo, murumque æquanti adhærebit, qui circulus intra se aliquot rotulas, 6. 8, vel plures habebit, quarum beneficio tectum abseque ullo negotio in quamcumque partem libuerit verti & circumduci poterit, ita ut fenestræ illi cœli plagæ observantur, ubi observatio instituenda erit. Observatione peractâ, claudantur fenestræ, ut instrumentum à pluviarum, ventorum vel aëris intemperie tutum sit & immune.
Cap. II.
De fabrica ipsius Quadrantis.
IN primis fiant ex firmo, solido & constanti ligno, duo parallelepipeda, ad longitudinem 4. vel 5. pedum, plus vel minus prout visum fuerit, eorum latitudo sit circiter 4 dig. Crassities v. 3. digit. Hæc parallelepipeda ab una parte ita connectantur, ut præcisè angulum rectum constituant, ab altera v. parte jungantur arcu quodam ligneo, ejusdē materiæ ; ejusdemq; latitudinis & crassitiei. Deinde optimè firmentur interius, pluribus lignis transversalibus, & inter se decussatim junctis, vel juxta delineationem appositam, vel alio modo, prout cuivi placuerit. Ut autem instrumentum justam firmitudinem & statum acquirat, debent omnes juncturæ ab utraque parte lamellis orichalcei(?)s obduci, limbus verò non solum in juncturis, sed totus ab utraque parte orichalco est muniendus. Huic limbo orichalco sic obducto & explanato debet adhuc alius limbus orichalceus ad exteriorem oram superimponi, & pluribus claviculis firmiter affigi, ut postea non dimoveatur, cujus
(58)
latitudo sit 1(?). dig. pro lubito, Crassities etiam arbitraria. Hic limbus quam optimè elaborari, expoliri & levigari debet, ita ut ejus facies superior à primo isto limbo ubique æqualiter sit elevata, ea parte v. quâ centrum respicit, ubique æqualiter ab eodem distet. Hoc facto, ex optimo & convenienti ligno fiat radius mobilis, seu regula, quæ à centro, circa quod moveri debet, usque ad limbum illum elevatum sese extendere debet. Circa centrum v. sicut & circa limbum, orichalco est obducenda. Huic regulæ adhærebit arcus quidam Orichalceus, cujus longitudo sit tanta, ut 61. limbi immobilis partes, (de quibus mox dicendum,) capere possit, non autem præcisè, sed paulum ultrà, qua de re dicetur postea. Latitudo hujus arcus potest esse 1. vel 1(?). dig. ejus crassities post elaborationem eadem erit cum crassitie limbi immobilis elevati, ut cum eodem prorsus unum constituat planum, & etiam cum illo quam exactissimè congruat, ita tamen ut circa eum movere possit, & quidem ubique æqualiter, ut nullibi quocunque moveatur, fiant hiatus, sed semper eidem erit contiguus.
Cap. III.
De hujus Instrumenti Divisione.
DUctis à centro duabus lineis rectis, quæ exquisitè angulum rectum constituant, spatium illud quod hæ lineæ in limbo immobili includunt,(?) dividatur in 90. gr & quilibet gradus in 12. partes omninò æquales.
Deinde in arcu illo mobili, qui regulæ adhæret
(59)
sumatur spatium, quod exactè 61. ejusmodi particulis limbi respondet, dividaturque illud in 60. partes æquales. Hujus spatii terminus unus erit linea fiduciæ in regula à centro instrumenti usque ad elevatum limbum sese extendens. Instrum. hac ratione diviso observari possunt quina quælibet minuta secunda. Nam cum quilibet gradus divisus sit in 12. partes æquales, valet quælibet pars 5 minuta prima. Deinde cum spatium illud in arcum mobili, quod 61. partibus in limbo respondet, divisum sit in 60.partes æquales, sequitur quod quælibet pars arcus mobilis in se contineat unam partem limbi cum talis partis. Sed jam quæritur, illa . unius partis in limbo, quantum valeat? (?). una pars limbi valet 5 minuta prima, redigantur ista ad minuta secunda per 60. fiunt 300". ut jam habeas , divide illa 300". per 60. habebis in quotp 5". pro , unde patet, cum dico unam partē arcus mobilis continere unam partem limbi cū . parte ejusdem; idem esse, si dicerem eandem continere 5 min. prima, & 5 sec. Videatur adjectum Schema in quo A B C D, sit pars limbi immobilis, arcus v. monbilis B C E F. B F, sit linea fiduciæ quæ à centro instrumenti per medium dioptræ usque ad limbum duci intelligatur. Cum jam Linea fiduciæ cum aliqua linea in limbo cincidit. etiam alteram lineam extremam scil. C E, cum alia coincidere necessum est, si modo rectè divisum sit instrumentum, linea autem F notata, quæ huic C E est proxima non coincidet cum linea G in limbo, quia pars illa quam absindit linea G, valet tantum 5 minuta prima, pars v. arcus mobilis, quam linea F abscindit, valet 5 minuta prima, & insuper 5. secunda distantia ergò quâ hæ duæ lineæ in-
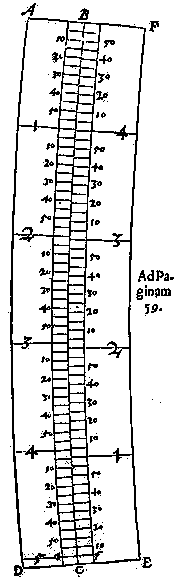
(60)
ter se discrepant, valet quinque minuta secunda. Si jam regula una cum arcu mobili tantum deprimi intelligatur, ut linea F coincidat cum linea G, tum per 5 minuta secunda mota est. Si v. tantum deprimatur, ut secunda linea arcus mobilis conveniat cum secunda linea limbi, mota est regula per 10 minuta secunda. Si tertia congruat, per 15". Si quarta, per 20". & sic consequenter, semper addendo 5". Si linea duodecima cum alia coinciderit, promota erit regula per unum minutum primum, quia una linea dat 5 secunda, ergò 12 lineæ dant. 60 secunda, id est. unum primum. Si decima septima linea arcus mobilis cum alia concurrat, mota erit regula per 1. primum & 25. secunda. Si vigesima quarta ; per 2 prima. Si 32 linea cum alia congruat, promota erit regula per 2 prima, & 40 secunda. Et sic de omnibus aliis.
Num rectè divisum sit instrumentum. nec ne, eodem modo explorari potest uti Astrolabium. de cujus examine, vide Cap. 3. partis primæ.
Instrumento ita diviso & examinato, apponendi sunt numeri, & quidem primò in limbo notandi sunt singuli gradus, incipiendo ab isto latere, quod horizonti parallelum erit, per totum limbum usque ad 90. Istæ lineæ, quæ gradus denotant, aliquantò longius deducendæ sunt, & numeris majusculis notandæ : reliquæ autem lineæ breviores, quia quælibet numeris notari, itidem à supperiore deorsum procedendo. In arcu v. mobili, quia semper partes in circulo mobili, numerantur in contrariam partem, respectu numerationis partium in limbo ideo incipiendum est à linea C E, parte scil. inferiore sursum versus, & primò quidem duodecimas quaslibet longius productas, nu-
(61)
meris majusculis, peculiari ordine notare, quibus minuta prima denotantur ; reliquæ autem breviores, & minuta secunda designantes minoribus numeris notandæ erunt, sed alternæ tantum, ut in limbo immobili factum est.
Hinc facile patet, quomodo in ipsa praxi, cujusvis anguli observati quantitatem deprehendere licet. Angulo enim observato, primum inspicienda est linea fiduciæ in regula, si ea exactè coinciderit cum aliqua ex longioribus in limbo, quæ scil. gradus denotant, tum statim Numerus asscriptus quantitatem anguli ostendet, & tunc neque prima, neque secunda minuta quærere oportet. Si v. cum aliqua ex brevioribus congruerit, numerus eidem asscriptus indicabit quot minuta prima præter gradus integros contineat angulus observatus. Si eadem linea fiduciæ non coinciderit cu aliqua linea in limbo, tum inprimis notandum quot gradus & minuta completa prætervecta sit, deinde inspiciendius est arcus mobilis & quærenda est linea, quæ cum alia congruat, (nunquam enim plure quam una congruere possunt) si infrà eam lineam sint aliqua minuta prima, quod alter numerorum ordo facile indicat, tum illa addenda erunt iis, quæ in limbo prius notata fuerunt, & numerus lineæ congruenti appositus, indicabit quot minuta secunda, præter gradus & prima, angulus iste comprehendat.
Sciendum autem est neminem esse astrictum ut semper quemlibet gradem in 12 partes dividat, sed potest eos in plures vel pauciores partes pro lubitu dividere, prout instrumentum majus vel minus fuerit. In minoribus enim instrumentis si quilibet gradus in 6 æquales partes divisus fuerit, valebit quælibet pars 10 minuta prima. & spatium in
(62)
arcu mobili quod 61. hujus modi partibus respondet dividatur in 60 partes æquales, notabit quælibet pars arcus mobilis in operatione 10. minuta secunda. Sic diviso quolibet gradu in 10. partes æquales, ut quælibet valeat 6 minut prima, valebit quælibet pars arcus 6 secunda : Nam quot minuta prima quælibet pars limbi continet, tot etiam minuta secunda dabit quælibet pars arcus mobilis, si modo illud spatium quod 61. partibus respondet, dividatur in 60 partes æquales. Si gradum quemvis diviseris in 15. partes æquales, valebit quælibet pars arcus mobilis 4 minuta secunda. In majoribus autem instrumentis si quilibet gradus in 20 partes æquales divisus fuerit, continebit quælibet pars arcus 3. minuta secunda. Si in 30. duo.
(63)
Cap. IV.
De Dioptris.
IN centro instrumenti collocandus est cylinder, cujus diameter A B sit circiter 1(?), dig. altitudo D A vel B C sit 2. vel 3. dig.

(64)
Deinde fiat dioptra E F G H, cujus latitudo &
altitudo excedant latitudinem & altitudinem Cylindri
semidigito. In hac dioptra fiant duæ rimulæ
I K, L M, ita ut spatium illud, quod inter illas
 comprehenditur, æquale sit diametro cylindri A B
vel D C. Deinde fiat alia rimula R S, reliquis in
transversum, tantum distans à basi dioptræ H G,
quanta est altitudo Cylindri D A. Cum rimulis
ita comparatum erit, ut dilatari & constringi pro
lubitu possint.
comprehenditur, æquale sit diametro cylindri A B
vel D C. Deinde fiat alia rimula R S, reliquis in
transversum, tantum distans à basi dioptræ H G,
quanta est altitudo Cylindri D A. Cum rimulis
ita comparatum erit, ut dilatari & constringi pro
lubitu possint.
Hæc dioptra regulæ mobili circa limbum instrumenti est affigenda ita, ut ejus medieas exactè insistat lineæ fiduciæ in regula tunc enim in ipsa praxi
(65)
si regula ita moveatur, ut stella per superiorem, rimulam visa, stringat superficiem Cylindri suprà, statimque per inferiorem rimulam visa, stringat superficiem Cylindri infrà, habebitur vera altitudo stellæ : si v. stella spectetur per rimulam transversam R S, & instrumentum huc illucque moveatur, donec stella per dictam rimulam visa, stringat summitatem Cylindri A B, tunc verum ejus habetur azimuth, quod quantum sit, regula in Circulo azimuthali (de quo postea) indicabit. Ad observationes v. Solis propter illius latitudine, oportet fieri incisuras quasdam, ut P Q & N O, quarū quantitas, quoad longitudinem, non tàm theoriâ, quàm ipsa praxi & experientiâ est inquirenda. Factis his incisuris, moveatur regula, donec per imum incisuræ videatur particula ex circumferentia solis, infra Cylindrum, tunc istæ incisuræ justam & debitam habent longitudinem, si v. major pars solis infrà spectetur, quam suprà, tunc sunt adhuc justo breviores, & tantillum adhuc excavandum, idque multoties repetitis experimentis continuandum, donec extremum circumferentiæ sive ambitus solis, æqualiter infra & supra Cylindrum videatur.
Debent autem istæ incisuræ inter se exactè esse æquales, aliàs praxis fallax & erronea erit. Eodem modo ad Rimulam R S, fiat rimula seu incisura V T, quæ planè ejusdem erit longitudinis cum prioribus Per cujus imum & summatitatem Cylindri A B, si spectetur extrema circumferentia solis, habetur verum ejus azimuth
(66)
Cap. V.
De illis rebus quibus instrumentum
sustentatur.
PRimò fiet axis sive columella ferrea, quæ in delineatione literis A B, notata est, huic axi Quadrans mediantibus duabus cochleis fixus adhærebit. Debet autē columella hæc omninò parallela esse isti quadrantis lateri, quod horizonti perpendiculare erit, alias quadrans nunquam ad perpendiculum collocari potest, ita ut semper ad perpendiculum maneat, quocunque vertatur. Pro axe hoc firmiter in suo loco superius tenendo, egrediantur è muro 5 ferramenta, quæ in centro concurrant, ubi erit foramen, cui superior axis extremitas inditur Quia v. antea dictum, quod murus debeat esse humilior ipso instrumento, debent ergò hæc ferramenta circa murum ita reflecti, ut supra instramentum ascendant, & deinde concurrant. Ut autem observator in suo opere nunquam ab his ferramentis impediatur, prodest ea ita fabrefieri, ut quodlibet eorum duabus firmetur cochleis, unâ circa murum, alterâ propè centrum, tunc enim observator illud quod sibi impedimento fore cognoverit, laxatis cochleis, eximere potest, relquis quatuor firmiter stantibus.
Et quia sunt 5, ablato uno, semper etiam pars opposita ab impedimentis vacua erit, quod non fieret, si numero essent paria. Hæc melius intelligi possunt ex figura hic apposita, quàm ex delineatione instrumenti.
Directè sub centro horum ferramentorum collocetut pedamentum quoddam literâ C notatum,
(67)
vel ex firmo & solido ligno, vel lapide, quod melius erit, in cujus summitate firmetur capsula quædam ferrea literis D E F G signata, inque ejus medio jaceat crassa quædam lamina ferrea vel orichalcea, quæ beneficio 4. cochlearum, in quamcunq; partem libuerit trudi & reduci potest, donec quadrans, qui mediante inferios axiis extremitate, ei insistit, quàm exactissimè ad perpendiculum sit collocatum, in quamcunque partem vertatur.
Cap. VI.
De Circulo Azimuthali.
NE instrumentum suâ perfectione destituatur construendus etiam est circulus azimuthalis, ut eodem negotio & altidudinē sideris supra horizontem, & ejusdē azimuth, sive distantiam à meridiano observare liceat. Construendus ergò est hic circulus ex firmo, constanti & solido ligno, tantæ amplitudinis, ut observator inter illum & quadrantis limbum liberè ambulare & res suas perficere queat. Limbus ejus eodem modo præparandus & orichalco obducendus est. Posteà in 360. gradus dividendus, initio facto à linea meridiana, quæ quàm accuratissimè in primis erit investiganda, quilibet gradus in 12. vel plures, pro ut visum fuerit, particulas est distribuendus. Regulæ axi & quadranti affixæ, arcus quidam adhaærebit, qui capiat 61. partes limbi immobilis, & in 60. partes æquales dividendus, ut fieri solet.
Circulus ipse 6, 8, vel pluribus columellis in-
(68)
cumbat, ut firmus & immutabilis semper in suo loco maneat. Ut autem observator majori commoditate omnia sidera, sive circa Zenith, sive circa horizontem constituta fuerint, observare possit, fiant scalæ sive gradus circum circa, jucta quadrantis limbum ita dispositi, ut observator in supremo grado stans sidera circa horizontem, in infimo vero sedens, sidera circa Zenith observare possit.
MEMBRUM II.
DE
Quadrantis Astron. Usu.
Problema I.
Lineam Meridianam invenire.
 D circulum azimuthalem rectè constituendum,
necessum est ut habeatur linea
meridiana, quæ sequenti modo invenitur :
In plano aliquo horizonti parallelom ex quocunque
puncto ducantur circuli quotcunque concentrici
non longè è se invicem distantes, è quorum centro
erigatur stylus, plano ipsi ad angulos rectos,
tantæ longitudinis, ut ejus umbra ad ciculos exteriores
sese extendat. Tum aliquot horarum spatio
ante meridiem observes umbram extremitatis
stili aliquem circulum tangere, quod punctum nota.
similiter cum extremita umbræ alium circulum
tetigerit, punctum iterum nota, & sic porrò
donec aliquot puncta, ad minimum tria, ante me-
D circulum azimuthalem rectè constituendum,
necessum est ut habeatur linea
meridiana, quæ sequenti modo invenitur :
In plano aliquo horizonti parallelom ex quocunque
puncto ducantur circuli quotcunque concentrici
non longè è se invicem distantes, è quorum centro
erigatur stylus, plano ipsi ad angulos rectos,
tantæ longitudinis, ut ejus umbra ad ciculos exteriores
sese extendat. Tum aliquot horarum spatio
ante meridiem observes umbram extremitatis
stili aliquem circulum tangere, quod punctum nota.
similiter cum extremita umbræ alium circulum
tetigerit, punctum iterum nota, & sic porrò
donec aliquot puncta, ad minimum tria, ante me-
(69)
ridiem observaveris : Eodem modo post meridiem, umbra crescente, denuò observa extremitatem umbræ, quæ ubi circulos anteà notatos attigerit, iterum notes.
Tandem connectantur bina ac bina in iisdem circulis puncta, lineis rectis, quæ orthogonaliter in duas æquales secentur partes, atque linea illa orthogonalis, erit linea meridiana quæsita. Si autem omnia puncta bisectionum non cadant in eandem lineam orthogonalem, falsitatem observationis arguent.
Nota.
Tempus prædicto modo lineam meridianam inquirendi, convenientissimum est circa solstitia, præsertim æstivum, tunc enim intra aliquot dies, insensibilis est declinationis solaris variatio, ibi-
(70)
demque radiorum refractio asmodum exigua, imò nulla.
Inventa hac ratione linea meridiana, & quadrante cum circulo azimuthali ad illam constituto, ulterius examinari potest, num exquisitè ea sit inventa nec ne. Aliquot horas ante meridiem, observa altitudinem solis simulque ejus azimuth. Regulà sic immotà manente, expecta donec sol post meridiem ad talem altitudinem perveniat, quo momento ejus azimuth nota. Si duo hæc azimutha æqualia fuerint, rectè constitutus est circulus azimuthalis, sin minus, corriendus. Idem potest etiam noctu fieri per stellas fixas.
Sunt & multi alii modi lineam meridianam inveniendi, quos omnes hic recensere, instituti ratio non permittit.
Problema II.
Elevationem Poli per stellas circum-
polares invenire.
COnstitueac firma quadrantem in linea meridiana, & observa altitudinem alicujus stellæ, in parte septentrionali (puta(?) unius de plaustro, vel ursa minore) tum post 12. horas eum eadem attigerit meridianum, infra vel contrà. Has altitudines adde, summæ dimidium dabit elevationem Poli quæsitam.
Sit e.g. B C, altitudo alicujus stellæ in plaustro ursa majoris, infra polum in meridiano sumptæ, 36,32'.24". Sit item B E altitudo ejusdem stellæ
(71)
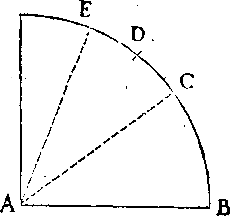
in meridiano supra polum, 74 15'.56". Si jam hi arcus addantur, erit summa 110. 48'.20". Cujus dimidium scil. 55. 24'.10". exhibet quæsitam poli elevationem, B D.
Nota I.
In observationibus astronomicis, si fieri potest nunquam observanda est altitudo stellæ, quæ minor est 20. gr. propter refractiones, quæ circa horizontem sunt majores.
Nota II.
Si detrahatur Elev. poli à 90. gr. residuum dabit elevationem æquatoris.
Problema III.
Altitudinem solis, Lunæ vel alterius
sideris deprehendere.
PRimo quadrantem ita move, ut per rimulam transversam, quæ extremitati Cylindri respondet, conspiciatur extimum circumferentiæ solis, extremitatem Cylindri stringens, tunc eodem momento moveatur regula ita ut per rimulam superiorem videatur tantillū circumferentiæ solis supra cylindrum, & tantundē etiam infra cylindrum per
(72)
rimulam inferiorem. atque ita & altitudinem & azimuth eodem negotio deprehendes. Altitudinem quidem in quadrante, numerando gradus & minuta prima in limbo immobili deorsum, minuta v. secunda in arcu mobili, qui regulæ est affixus, idque in contrariam partem, id est, sursum. In circulo azimuthali dabitur azimuth, si numerentur gradus & minuta prima in limbo immobili, incipiendo à linea meridiana, in arcu v. qui regulam comitatur, in contrariam partem numeranda sunt minuta secunda. Qui meliorem explicationem horum desiderat videat cap. 3. membri præcedētis.
Nota.
Quandocunque observas altitudinem Solis, Lunæ vel stellarum, (Planeta quinqua reliqui easdem cum sstellis fixis habent refactiones.) tum semper ab altitudine observata subtrahe refracionem, & ed residuum (puta in Solis & Luna observationibus tantum) adde illorum parallaxin, & habebis altitudinem veram & correctam.
| Sit e.g. observata altitudo Solis | 19.30'. 0". |
| Hinc subtrahe refractioneonem(sic) Solis | 4.45. |
| - | |
| Residuo- | 19.25. 15. |
| Adde parallaxim Solis- | 2. 43. |
| - | |
| totus erit Altitudo correcta | 19.27.58. |
Problema IV.
Obliquitatem Zodiaci investigare.
Ob(sic)serva in utroque solstitio altitudinem solis meridianam, eamque corrige per præcedens
(73)
problema, tum aufer minorem altitudinem correctam à majori itidem correcta, relicti dimidium dat obliquitatem Zodiaci, id est, maximam declinationem Solis ab Æquatore.
Nota.
Ex hac observatione datur etiam elevatio poli. Nam si obliquitatem inventam auferas à majori altitudine, vel subtrahas à minori, habebis elevationem Æquatoris, cujus complementum ad 90 gradus, dabit elevationem Poli.
Alius modus prædictam obliquitatem
invenire.
Inquire primum altitudinem Poli, quâ inventâ, datur etiam elevatio æquatoris, quam si auferas ab altitudine Solis meridiana in solstitio æstivo observata ; relinquetur obliquitas Zodiaci. Vel si altitudinem correctam Solis solstitio brumali acceptam, subtrahas ab elevatione æquatoris, residuum ostendit iterum maximam declinationem Solis.
Problema V.
Locum Solis in Ecliptica invenire.
COgnitâ elevatione Poli, observa altitudinem Solis meridianam, eamque corrige per problema 3. Si altitudo Aolis major fuerit sublimitate Æquatoris, Sol erit in semicirculo bore, aufer hanc ab altitudine observata, residuum ostendet declinationem Solis borealem. S v. altitudo Solis minor fuerit altitudine æquatoris, aufer altitudinem Solis ab altitudine æquatoris relinquetur
(74)
declinatio Solis australis. Data Solis declinatione, datur etiam ejus locus in Ecliptica per 1. axioma Triang. Sph. Pitisci.
Notæ.
- 1. Si Sol est in semicirculo boreali ascendens, erit latus inventum ipsa longitudo Solis, ab æquinoctio verno.
- 2. Si Sol est in semicirculo boreo descendens, Latus inventum subtrahatur à 180 gr. residuum ostendet locum ab æquinoctio verno.
- 3. Si Sol est in semicirculo australi descendens, inventum latus est distantia Solis ab æquinoctio autumnali, cui addantur 180. gr. ut habeatur locus ab æquinoctio verno.
- 4. Si Sol est in semicirculo australi ascendens, inventum latus subtrahere ab integro circulo, residuum dabit locum ab æquinoctio verno.
Exemplum ad primam Notam.
Anno Christi 1643. 18. Aprilis observata altitudo Solis meridiana 48.41'.20". quæritur Locus Solis in meridiano qui est Lugd. Batav. sub latitudine 52.10'(?)? Corrigatur in primis altitudo Solis per probl. 3.
Et quia in tali altitudine nulla datur refractio, ideo addatur tantum parallaxis, quæ est, 2'.0",
| Altit observata. | 48.41'.20". |
| Parall. addenda | 2.0. |
| - | |
| altit. Solis correcta. | 48.43.0. |
Iam quia altitudo Solis sub data latitudine, major est altitudine æquatoris, ideo hæc ab illa est
(75)
| Altit observata. | 48.41'.20". |
| Parall. addenda | 2.0. |
| - | |
| altit. Solis correcta. | 48.43.0. |
Fiat ergò juxta axioma priùs citatum : ut 100000. ad 250533. (secant. compl. ang. 23.31'.30".) ita 18905. (sinus lateris dati, 10 53'.50".) ad 47363. (sinum arcus quæsiti 28.16'.13". est ipsa longitudo Solis ab æquinoctio verno. ut habet nota 1.
Exemplum ad Notam II.
Anno 1642 19. Iulij, observata est altitudo Solis in meridiano Lugd. Bat. 58.42'.20". quæritur quonam in Ecliticæ loco Sol tum erat constitutus? Primio corrigetur altitudo observata ut prius.
| Altit. observ. | 58.42'.20". |
| Parall. add. | 1.55. |
| - | |
| Altit. correc. | 58.44.15. |
| hinc subtrahatur Elevatio Æquat. | 37.49.30. |
| - | |
| ut maneat decl. Solis bor. | 20.54.45. |
Dic jam, ut 100000. ad 250533. (sec. compl. 23.31'.30".) ita 35695. (sinus lateris, 20.54'.45". ad 89428. (sin. arcus quæsiti 63.25'.) qui à 180. est subtrahendus, quia Sol erat in semicirculo boreo descendens, manebit longitudo Solis æquinoctio verno, 116.35'.
(76)
Non aliter in aliis exemplis est procedendum, dummodo observvetur quid quælibet prædictarum notarum præcipiat.
Problema VI.
Declinationem stellarum invenire.
COgnitâ Elevatione Poli, observa altitudinem cujuscunque stellæ meridianam, quæ si major fuerit elevatione æquatoris, subtrahatur ab illa altitudo æquatoris, residuum dabit declinationem borealem. Si v. altitudo stellæ minor fuerit altitudine æquatoris, subtrahatur illa ab hac, residuum dabit declinationem stellæ australem. Memor esto, quod quotiesunque altitudo stellæ observata minor fuerit 20. gr. corrigenda est per subtrctionem refractionis.
Problema VII.
Ascensionem rectam Solis invenire.
EX data declinatione Solis & obliquitate Zodiaci, invenitur ascensio recta Solis per axio, 2. Sphær. hoc modo : ut Radius ad tang. ang. 23.31'. 30". ita tang. compl. lateris dati, ad sec. compl. Lat. reliqui, cujus arcus dabit ascensionem rectam Solis.
Nota.
Etiam hic observandæ sunt quatuor illæ Requlæ suprà problemati quinto adjectæ.
(77)
Problema VIII.
Ascensionem rectam stellarum in-
vestigare.
OBserva altitudinem meridianam Solis, & per antecedens problema, inquire ejus ascensionem rectam, habeasque ad manus, horologium exactissimum, in minuta secunda etiam distributum,(?) quod dirige eo momento quo Solis accipis altitudinem, in horam 12. Observa deinde stellam cujus ascensionem quæris, donec veniat etiam in meridianum, ubi ejus altitudinem sume (unde habebis ejusdem declinationem per probl 6.) ac simul inspice quodnam tempus horologium ostendar, hoc ipsum resolve in gradus & minuta æquatoris, per tabulā, cujus Titulus : Canon convers. &c. quibus adde ascensionē rectam Solis, summa dabit ascensionē stellæ quæsitam. Si quandoq; accidat ut hæc summa 360. gr. superet, abiice ab illa totam circumvolutionem circuli, residuū dabit quod quæris.
Problema IX.
Data ascensione recta & decl. stellarum, ea-
rundem Latitudinem & Longit. invenire.
Declaratio Schematis
A Polus mundi boreus. B Polus Eclipticæ boreus. G D E I, Æquatuor. H D F K, Ecliptica.
(78)
E C, declinatio stellæ borealis. D E, asc. recta,
D F, Longitudo stellæ. C F latitudo ejusdem bo-
 realis. D. principum arietis. H G B A K I, Colurus
Solistitiorum.
realis. D. principum arietis. H G B A K I, Colurus
Solistitiorum.
Exemplo res erit clarior.
Data est declinatio Capellæ, 45.30'. borealis, unà cum ascensione recta, 71.49'. observata anno Christi 1600. à Tychone Brahe, quæritur ejus Latitudo & Longitudo ? Latitudo sic inquiritur : in triangulo A B C, datur latus B A, nempè distantia Polorum, 23.31'.30". datur itidem latus C A, utpotè compl. declinationis stellæ, ad 90. gr. 44.30'. Angulus B A C hoc modo datur:
Compl. ascensionis rectæ D E ad 90. erit arcus E I, 18.11'. hunc aufer à 180. residuum dabit angul. B A C quæsitum, 161.49'. quo cognito operare juxtà axio. 4. Triang. Sphær. Pitisci invenies latus, B C, cujus compl. ad 90. C F, dabit latitudinem quæsitam 22.51'.30".
(79)
Longitudinem autem hoc modo inquires : in eodem triangulo A B C, invento latere B C, inquire ang. A B C, per 3. axio. Sphær Cujus amplitudo erit F K, hunc aufer à 90. gr. residuum dabit arcum D F, ipsam longitudinem stellæ quæsitam...
Nota.
Si ascendsio recta fuerit 90. gradibus minor, Longitudo stellæ erit in quadrante primo, si v. major, & minor quam 180. erit in quadrante tertio. Si v. inter 270. & 360. fuerit, in quadrante quarto seu ultimo erit Long. sti(sic)llæ.
Operatio ipsa præced. Exempli.

Quia triangulum A B C est obtusangulum, ut facilior fiat operatio, demittatur perpendiculum. B L, ex puncto B, & producatur C A in L, dabiturque triangulum B L A, rectangulum, in quo cogniti sunt duo anguli, scil. B L A, rectus, & B A L, qui est compl. ang. B A C ad 180. Cognitum quoque est latus A B, quarè per ax. 1. Sphær. sic dico : ut 100000. ad 39914. (sin. lateris A B, 23.31'.30".) ita 31205 (sinus ang. L A B, 18.11.) ad 12455. (sinum lateris oppositi B L, 7.9'.18".)
Hoc jam invento quære latus L A, per 2. ax Sphær. dicendo : ut 100000. ad 95006. (sinus
(80)
compl. ang. L A B,) ita 43532 (tang. basis B A) ad 41358. (tang. Laterus L A.) scil. 22.28'.8". Adde jam latus L A, lateri A C, 44.30'. habebis rectangulum B L C, in quo notum est latus L C, 66.58'.8". item latus B L, 7.9'.18". & angulus B L C rectus. Ut jam inveniatur latus B C, dic juxta 1. ax. ut 100000. ad 100784. (sec Lat. B L.) ita 255603. sec. alterius lat. L C.) ad secantem basis B C, 257429. est igitur latus B C, 67.8'.30". Invento itaque latere B C, si sumatur ejus compl. ad 90. habebitur arcus C F in Schemate, ipsius nimirum stellæ latitudo 22.51'.30".
Porrò pro Longitudine ejusdem stellæ invenienda, scire oportet amplitudinem ang. A B C, in dato triangulo B C A, qui hoc modo investigatur : quæratur primò in triangulo B L C, ang. ad B, per ax. 2. Sph. ut 100000. ad 802805 (sec. compl. lat B L) ita 235229. (tang. lat. L C.) ad 1888571. (tang. ang.opp L B C, 86.58'.8".)
Hoc angulo invento, inquiratur etiam in triangulo B L A, angulus L B A. per idem ax. hoc modo : ut 100000. ad 109064 (sec. lat B A) ita 304450. (tang. compl. ang dati) ad 332045. tang. ang. reliqui L B A, 73.14'.22". qui ab angulo L B C, subtractus, relinquet angulum A B C, 13. 43'.46". Cujus mensura est arcus F K, in Schemate, qui auferendus est à 60. gr. residuum dabit ipsam Longitudinem stellæ à D puncto æquinoctii verni seu principii arietis, 76.16'.14". vel, 16.16'.14". II.
(81.)
Problema X.
Data Longit. & Latitudine ; Ascensionem
rectam & Declinationem invenire.
QUia hoc problema nihil est aliud quàm antecedentis
conversum, nullum hic adhibetur
 exemplum, sed modus tantum inveniendi ea quæ
hic quæruntur.
exemplum, sed modus tantum inveniendi ea quæ
hic quæruntur.
Declarationem Schem. vide probl. antec.
In triangulo B A C, datur Latus B A, dist. scil. polorum, datur quoque latus B C, videlicet complem. Latitudinis ad 90. gr. Datur etiam angulus C B A, compl. nimirum Longitudinis D F ad 90. & quæritur ang. B A C, qui per 3. ax. Sph. invenitur. Sinus enim laterum, sinibus oppositorum angulorum directe sunt proportionales, quo invento, si ab eo subtrahatur quadrans G D, remanebit ascensio recta D E.
(82)
Quæritur etiam latus A C, quod per idem axioma invenitur, cum ang. oppositus C B A, sit cognitus. Latere hoc invento, & à 90. gradibus subtracto, restabit C E, decl. quæsita.
Multa ac varia problemata, pro varietate datorum hic possent adferri, sed brevitati studens, ea consultò prætereo.
Problema XI.
Distantias stellarum invenire.
POssunt quidem distantiæ stellarum per calculum, ex dta ascensione recta & declinatione inveniri, sed multò facilius absque calculo inveniuntir per Sextantem aliquem Astronomicum, qui eodem prorsus modo, quo quadrans Astronomicus, fabricandus, quoad divisionem scilicet, regulam, pinnacidia & Cylindrum in centro. Cujus Limbus non quartam sed sextam tantum circuli partem continebit, unde etiam nomen habet. Prætereà etiam ad alterutrum latus habebit dioptram immobilem, in regula mobili alteram, utrique respondebit Cylinder in centro.
In hujus instrumenti praxi duo requiruntur observatores, quorum unus instru. ita dirigit, ut unam stellam videat per dioptram ad latus immobilem, alter v. regulam movet, ut per ejus dioptram conspiciatur stellarum observandarum altera, ut in limbo & arcu mobili habeatur distantia earum in gradibus & minutis primis & secundis, non secus ac in quadrante.
Nota.
Hoc instrumentum non ad perpendiculum fixum hærebit, ut quadrans, sed ita summitati cu-
(83)
jusdam Columnæ incumber, ut commodè pro arbitrio, in hanc vel illam partem inclinari & reclinari possit, ut in ipsa praxi ejus planum semper coincidat cum linea recta, quæ duci intelligitur inter duas stellas, quarum distantia quæritur.
Problema XII.
Longit. & Latitudinem Planetæ, vel alte-
rius cujusdam novi sideris, exduarum
Stellarum distantia, Longitudine ac
Latitudine cognitis, invenire.
Explicatio Schematis

A Polus Eclipticæ boreus. B, sinistrum genu Ophiuchi. C, dextrum genu ejusdem. G, Venus. G C, distantia ejus à dextro genu. G B, dist. à sinistro. B C distantia dictarum stellarum. B E latitudo borea sinistri genu. B A ejusdem compl. ad 90. gr. C D, Latitudo borea dextri genu. C A, ejus compl. E D, differentia Longitudinum datarū stellarum.
In hoc Schemate dantur B C, dist. stellarū, 9. 28'.12". G C, distantia Veneris à dextro genu
(84)
Ophiuchi, (per obs. inventa) 9.25'.0" G B distan. ejusdē à sinistro genu, 8.39'.0". C D Latit. dextri genu borea, 7.18'.0". C A ejusdē cōp. ad 90. 82. 42'.0". E B, latit sinistri genu borea, 11.30'.0". A B ejus cōpl. 78.30'.0". Datur etiam D E diff. Longit. datarum stellarū 8.45'. & cum idem arcus E D sit mensura ang. B A C, & ipse erit 8.45'.0".
Quæratur jam in triangulo C A B, (cujus tria latera cum ang. B A C, cognita sunt) ang. A B C per 3. ax. Sph. sic ; ut 16452. (sin lateris B C 9.28'. 12".) d 15212 (sin. ang. B A C, 8.45') ita 99189. (sinus lat. A C, 82(?).42'.) ad 9172(?)3. (sinum arcus 66.30'.38".) & quia ang. qui quæritur obtusus est, ideò sumendum est complementum arcus inventi ad semicirculum, erit angulus A B C, 113.29'.22". Deinde in triangulo B G C, quæratur ang. G B C, per 4 ax. Sph. dicendo : ut 100000. ad 16452 (sin. rect. Lat. B C, 9 28'.12".) ita 15040. (sinus rectus lat alterius B G 8.39') ad 2474 quartum. Et ut 2474 quartus, ad 100000. ita 1337 (diff sin. versorum lat. tertii & diff. reliquorum laterum) ad 54042. (sin. versum ang quæsiti, 62.38'. 25".) Addantur jam ambo anguli inventi, erit summa 176.7'.47". pro angulo A B G, cujus complementum ad 180. dat ang G B H, 3.52'.13". Demissa igitur perpendiculari G H, quæratur amplitudo arcus G H, per 1. ax. Trian. Sph. ut 100000. ad 15040. (sin. basis seu hypothenusa) ita 6748. (sinus ang. H B G, 3.52'.13".) ad 1015. (sinus lateris opp. G H, 0.34'.54".) In eodem triangulo quæratur H B, dicendo : ut 100000. ad 99772 (sin. compl. ang. H B G) ita 15213. (tang. basis B G,) ad tang. lat, op H B, 15178. Cujus arcus est, 8.37'.43". pro H B. Addantur porrò H B & B A. summa dabit arcum H A, 87.7'.43". Deinde in triangulo H A G, quæratur latus A G,
(85)
sic : ut 100000. ad 1996252. (sec. lat. H A,) ita 100005. (sec. lat. G H, 0.34'.54") ad 1996352. (sec. basis G A, 87.7'.23".) cujus compl. ad 90. dat arcum G F, ipsam Latit. Veneris borealem quæsitam 2.52' 37". Quæratur etiam in eodem triangulo, angulus G A H, ita : ut 100000. ad 100126 (sec. compl. lat. G A.) ita 1016. (sinus lat. G H 0.34'.54".) ad 1017.(sin. ang. G A H, 0 34'.56".) qui additus ad longitudinem sinistri genu Ophiuchi litera B signati, (quæ est 4.14'.44" ♐︎) dabit veram Long. Veneris, 4.49'.38". ♐︎.
Problema XIII.
Datis duarum stellarum in eodem azimu-
tho existentium distantia, & alterutrius al-
titudine; elevationem Poli invenire.
Declaratio Schematis
A Polus mundi, K vertex seu Zenith, E D C B
 Horizon. F G C L æquator. K I H D circulus
Horizon. F G C L æquator. K I H D circulus
(86)
verticalis. H I, distan. stellarum I D, altitudo stellæ superioris. G I, declinatio stellæ in I, sitæ. H D altitudo stellæ inferioris, A K, Distantia Poli à verticè. A B elevatio Poli, quæ quæritur.
In triangulo itaque A I H, dantur omnia Latera. Latus enim H I, est distantia stellarum, quæ nota præsupponitur, I A, compl. declin. stellæ ad I. Latus A H, compl. alterius stellæ, ad H sitæ. (si una stellarum sit in ipso æquatore, latus illud erit 90) Quæretur ergò in hoc triangulo, angul. A I H, eo modo, quo ex tribus lateribus in antecedente problemate factum est. Quo invento, in triangulo A K I, iterum tria erunt nota, ang. enim K I A, est anguli jam invemti compl. ad semicir. Latus A I, datum est in priori triangulo. K I v. est comp. altitudinis stellæ superioris ad 90. Si autem datur stellæ altitudo ad H, Subtrahatur ab ejus complemento distantia stellarum, residuum dabit latus K I. Qua propter in hoc triangulo inveniatur latus K A. ac inventum à quadrante subtrahatur, residuum ostendet Elevationem Poli quæsitam.
Problema XIV.
Data declinatione duarum stellarum in
eodem cognito Almucantharat sitarum,
elevationem Poli invenire.
Explicatio Schematis
A polus mundi. H Zenith. F E D G Horizon, E B altitudo stellæ unius, D C alt. alterius, priori æqualis. H B & H C complementa altitudinum
(87)
stellarum, B C, earundem distantia. B A, compl. decl. stellæ in B. C A, complementum declinationis stellæ in C.

In triangulo itaque H B C, ex tribus lateribus cognitis, inveniatur ang. B C H ; & in triangulo B A C, similiter ex tribus lateribus notis inveniatur angulus B C A, à quo subtrahatur angulus B C H, manebit ang. H C A. Si jam in triangulo H C A, ex duobus lateribus & angulo uno cognotis, inveniatur latus H A, habebitur elevatio Poli desiderata, hujus nimirum complementum, ad. 90.
Problema XV.
Data temporis articulo, cum phænomeni novi
altitudine & azimuthali gradu simul obser-
vandis : datur ejus ascensio recta atque de-
clinatio, & ideoque etiam ejusdem Long. & Latit.
SIt in diagrammate apposito M K N, Horizon. M L A B N, meridianus L H K, quadrns æqua-
(88)
toris, cujus polus B. Polus autem Horizontis A.
Detur ex observatione, C G, altitudo cujusdam
phænomeni in C existentis, item M G, distantia
 ejus in horizonte à meridiano. Denique punctum
L. Medii sc. Cœli in æquatore, quod adhibita ascensione
recta Solis cognoscitur ex effluxu temporis
inter meridiem diei antecedentis aut consequentis,
& momentum observationis habitæ, si
horas & horarum minuta, ex horologio, vel altitudine
alicujus stellæ cognita, in gradus & minuta
æquatoris resolveris.
ejus in horizonte à meridiano. Denique punctum
L. Medii sc. Cœli in æquatore, quod adhibita ascensione
recta Solis cognoscitur ex effluxu temporis
inter meridiem diei antecedentis aut consequentis,
& momentum observationis habitæ, si
horas & horarum minuta, ex horologio, vel altitudine
alicujus stellæ cognita, in gradus & minuta
æquatoris resolveris.
Cum itaque in triangulo A B C cognita sint latera A B, (compl. Elevationis Poli) & A C, compl. altitudinis phænomeni observatæ unà cum angulo C A B, compl. azimuth observati G M, ad semicirculum, ideo manifestabitur latus C B, quo ex 90. gr. subtracto, relinquetur declinatio quæsita C H, Cognitis jam omnibus lateribus in triangulo A B C, angulus C B A, id est, H L, latére non potest. quo addito ad ascensionem rectam anteà è tempore inventam, si phænomenon in orientali plaga observatum fuerit, vel subducto, si idem in parte à meridie occidua hæserit, etiam ascensio recta sideris ignoti manifesta erit. Quibus ac-
(89)
quisitis, Longitudo & Latitudo ejusdem è præcedentibus problematibus derivantur.
Problema XVI.
Data altitudine Solis ejusque declinatione
cum elevatione Poli ; datur momentum tem-
poris in horis ac minutis correspondens. Et Contrà.
Casus I.
Si Sol in æquatore, hoc est, in principio ♈︎ vel ♎︎.
SIt Sol in principio ♎︎ ad punctum H, & sit ob-servata ejus altitudo, H L, 34 9'.27". & quæratur
quota sit hora diei, id est, quantus sit arcus
 A H ? vel angulus A F H ? quo arcu vel angulo
Sol tunc distat à meridie. Quia nota supponitur
A H ? vel angulus A F H ? quo arcu vel angulo
Sol tunc distat à meridie. Quia nota supponitur
(90)
poli elevatione K F, 49.35', ideo nota est etiam altitudo æquatoris I A, æqualis compl. Elevat. Poli 40.25'. Atque adeo in triangulo H E L, dantur duo anguli nempè rectus ad L, & acutus ad E, cujus mensura est arcus A I, & denique Latus H L, altitudo Solis. Hinc invenitur arcus H E, 60.0'. Cujus complementum ad 90. est arcus H A, 30. qui ostendit solem duabus horis à meridie distare, hoc est, esse vel 10. antemeridianam, si altitudo Solis crescat, vel secundam pomeridianam si eadem decrescat.
Casus II.
Si Sol sit in aliquo signo boreo.
Sit Sol in 15. gr. ♉︎ (?) ad punctum H & observata
sit ejus altitudo supra Horizonetem H L, 48.
 41'.33". quæretur autem quota sit hora diei, hoc
est, quantus sit arcus M A, vel ang. M F A ? quo
41'.33". quæretur autem quota sit hora diei, hoc
est, quantus sit arcus M A, vel ang. M F A ? quo
(91)
arcu vel angulo Sol tuu(sic)c à meridie distat. Quia nota præsupponitur Elev. Poli, 49.35'. notum etiam est ejus compl. ad 90 F G, sc. 40.25'. Nota item supponitur declinatio Solis H M, 16.21'. Cujus compl. ad 90. est H F, 73.39'. Datus quoque est arcus G H, 41.18'.27". utpote compl. altitudinis Solis observatæ, 48.41'.33". Itaque in triangulo F G H, omnia latera sunt nota, unde inquiritur ang. desideratus G F H. 30. grd. Quarè iterum Sol duarum horarum spatio à meridiè abest.
Casus III.
Si Sol sit in signo aliquo australi.
Sit Sol in principio ♏︎, ad punctum H, & sit
observata ejus altitudo H L, 23.30'.45". quæra-
 tur autem quota sit hora diei, sive quantus sit arcus
A M ? Quia nota est Elev. Poli 49.35'. notum
tur autem quota sit hora diei, sive quantus sit arcus
A M ? Quia nota est Elev. Poli 49.35'. notum
(92)
est etiam ejus compl. F G, sive N O, 40.25'. nota item præsupponitur decl. Solis H M, 11.29'. ergò notum est ejus compl. H N, 78.31'. Nota quoque ex observatione est altitudo Solis H L, 23. 30'.45". erit itaq; compl. ejus H G, 66.29'.15". Vel arcus H O ex altitudine Solis H L, & quadrante L O compositus 113.30'.45". Atque sic in triangulo F G H, nec non in triangulo opposito N H O, nota sunt omnia lateri. Quæratur itaque ang. G F H, in triangulo H G F, cujus mensura est arcus A M. Vel quæratur ang. H N O, in triangulo opposito, quo invento & à 180. gr. subtracto, manebit angulus A N M. cujus mensura est idem arcus A M, qui quærebatur, ille enim est, qui ostendit quantum Sol à meridiano distet.
Problema XVII.
Data ascensione recta Solis unà cum ascensio-
ne recta ac declinatione alicujus stellæ, ejusque
altitudine observata sub certa Elev. Poli ;
datur tempus nocturnum correspondens.
SIt ad 13. diem Sept. altitudo lucidæ ♈︎ per quadrantem observata 25. gr. in parte cœli orientali. Datur autem Longitudo ejus 2.14'. ♉︎(?). Latitudo 9.57'. borealis, quare declinatio erit 21. 36'. & ascen. recta, 26.21'. Ergò in appositi diagrammatis triang. A B C data sunt omnia latera, A B, 37.50'. distan. Polorum. B C, 68.24'. compl. decl. stellæ. A C 65.0' compl. altit. observatæ C E, dabitur ergò ang. A B C, 76.38'. cujus mensura est arcus quæsitus D F, quo subducto ab ascensione recta Lucidæ ♉︎(?), 26.21'. cir-
(93)
culo integor prius addito, remanebit ascensio recta
medii cœli 309.43'. à qua rursum sublata asc.
 recta Solis 181.50'. relinquetur arcus inter medium
cœli & solem, 127.53'. qui in tempus conversus,
dat horas 8. min. 31. Si v. in parte occidentali
alt. stellæ observetur, addendus est arcus
quæsitus asc. rectæ stellæ, ut constet asc. recta medii
cœli.
recta Solis 181.50'. relinquetur arcus inter medium
cœli & solem, 127.53'. qui in tempus conversus,
dat horas 8. min. 31. Si v. in parte occidentali
alt. stellæ observetur, addendus est arcus
quæsitus asc. rectæ stellæ, ut constet asc. recta medii
cœli.
Problema XVIII.
Data Phænomeni circa polum mundi semper
conspicui, utraque altitudine meridiana ; da-
tur aggregata utriusque altitudinis Paral-
laxis, si quam habuerit, vel Differentia.
ARduam & intricatam Parallaxium doctrinam ex professò & theoreticè tractare, non est hujus loci, sed ex Astronomia ea est petenda, &
(94)
jam tanquam nota & cognita præsupponitur. Hic pauca quædam attingamus, quæ ipsam praxin spectant, quomodo scil. instrumento nostro, explorare possimus an phænomenon aliquod apparens, parallaxin habeat nec ne, & si habuerit, quanta sit illa ; & quanta etiam sit differentia ejusdem in utraque altitudine meridiana. Nam omne Phænomenon parallaxin habens, quò propius fuerit Horizonti, eò minorem, donec perventum sit ad ipsum verticem, ubi omnis parallaxis prorsus evanescit.
Intelligendum est problem propositum de tali phænomeno, quod una cum stellis fixis sit immobile. Si v. mobile fuerit, reducetur ad immobilitatem per mutationem declinationis ejus, in diurno motu observandam & proportionaliter acco (sic) modandam.
Præsentis problematis Casus duo sunt : aut enim phænomenon polum mundi ita circumit, ut semper infra verticem loci ad boream in utraque altitudine meridiana conspiciatur. aut in superiore altitudine verticem superat, & ad meridiem vergit. Ubi notandum, quod in casu priori differentia utriusque distantiæ à polo, sit ipsa summa parallaxium, in posteriori verò eadem differentia distantiarum phænomeni à polo, sit parallaxium differentia.
Exemplum Casus prioris.
Sit A centrum mundi, B locus observatoris in superficie terræ, D H O, orbis stellarum fixarum, H polus mundi, C I M P, orbis novi phænomeni, cujus alt. meridiana maxima est P I, sive Q I, minima v. P M, sive Q M, Nam lineæ B Q N & A P O coincidere intellìguntur, propter insensibi-
(95)
lem comparationem diametri terræ, ad diametrum octavæ sphæræ.

Sit jam Elevatio poli 52 gr. altitudo meridiana inferior in M, observata sit, 22.20'. superior v. in I, 79.40'. Subtrahatur ergò altitudo phænomeni minor, ab elevatione Poli, manebit distantia minoris altitudinis à polo 29.40'. Deinde subtrahatur elevatio poli ab altitudine phænomeni maxima, remanebit ejusdem à polo distantia 27.40'. harum distantiarum differentia, scil. 2.0'. est parallaxium summa.
Exemplum Casus II.
Sit phænomenon aliquod, cujus altitudo inferior in D observata 15.25'. ad elev. poli 60. gr.
(96)
superior v. altitudo verticem superans, ut in C sit
100.30'. Subtrahatur ergò ut prius altitudo minor
ab elevatione poli, restabit distantia ejus à polo
44.35'. deinde subtrahatur elevatio poli ab altitudine
majore, manebit iterum distantia earū 40.30'.
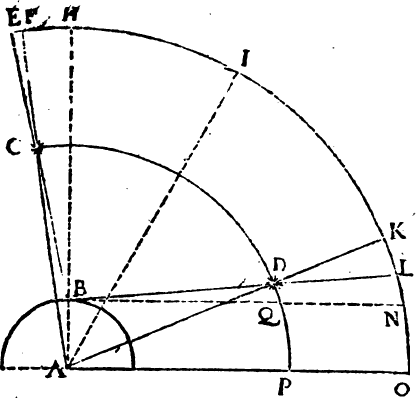 Subtrahatur jam distantia minor à mo(sic)jori, ut maneat
earum differentia 4.5'. quæ etiam est differentia
parallaxium. Ex his quæ in utroque Casu
dicta sunt construi potest sequens
Subtrahatur jam distantia minor à mo(sic)jori, ut maneat
earum differentia 4.5'. quæ etiam est differentia
parallaxium. Ex his quæ in utroque Casu
dicta sunt construi potest sequens
REGULA:
Subtrahatur altitudo phænomeni infima(?) ab elevatione polis, residuum servetur : deinde Subtrahatur elevatio polis ab altitudine phænomeni su-
(97)
prema, residuum iterum servetur. Horum residuorum differentia est parallaxium summa in casu priori, in posteriori v. est earundem differentia.
Problema XIX.
Data parallaxiam summa vel earum
differentia, ipsas parallaxes invenire.
REpetatur exemplum Casus prioris, ubi inventa est summa parallaxium 2.0'. inquirendum jam est quanta sit quælibet parallaxis seorisim(sic), quod hoc modo fieri potest.

Ponatur A B 1000. & assumatur alia linea A R cujuscunque magnitudinis, v. gr. 2000, ut fiat
(98)
triangulum A B R, item A S, ejusdem magnitudinis, & constituatur triangulum A B S. in his triangulis inquirantur per 2. ax. plan. anguli B R A & B S A, Nam dantur in quolibet horum triangulorum duo latera, & angulus majori lateri oppositus. Si enim subtrahatur altitudo phænomeni minor 22.20'. à 90. remanebit angulus L B D, 67.40'. Cujus complementarum ad duos rectos est angulus A B S, 112.20'. Item subtracta à 90. altitudine majore G N, 79.40'. restabit angulus D B G, 10. 20'. Cujus complementum ad semicirculum est angulus R B A, 169.40'.
Facta operatione, erit angulus B R A, 5.8'.41". & angulus B S A 27.41'.53". His angulis inventis, facile inveniuntur parallaxes, id est, anguli B E A & B M A. Nam ut se habet angulus B R A, ad angulum B E A ; ita angul(sic) B S A, ad angulum B M A. Et componendo. ut summa duorum angulorum inventorum ad angulum minorem (vel majorem) ita summa parallaxium prius inventa, ad parallaxin minorem (vel majorem) Tali operatione peractâ, erit angulus parallaceos superioris B E A, sive F E G, 18'.54". angulus vero parallaxis inferioris B M A, sive K M L, 1.41'.6". quæ parallaxes si addantur, eandem prorsus summam restituent, quæ prius erat inventa, scil. 2.0'.0".
Non adeò dissimilis ratio est parallaxes invenire ex data differentia.
Resumatur figura Casus posterioris, ubi inventa est differentia parallaxium, 4.5'. Constituantur duo triangula, ut prius. A B R, & A B S, & sit latus A B, iterum 1000. & A R & A S 2000. Anguli A R B & A S A, eodem modo inveniuntur, quo in præcedenti exemplo sunt inventi. quo facto erit angulus A R B, 5.13'.19". Angulus
(99)
verò B S A, 28.49'.0". quorum differentia est,
23.35'.41". Iam dico : ut A R B, ad A C B ;
ita B S A ad B D A, & dividendo ut differentia
angulorum inventorum, ad angulum minorem,
(vel majorem) ita differentia parallaxium inventa, ad
parallaxin minorē, (vel majorem) Terminis ad minimam
denominationem reductis, & operatione
 peracta, proveniet parallaxis supperior E C G,
0.54'.13". inferior verò K D L 4.59'.13". quæ si ab
invicem subtrahantur, manebit earum dif(sic)erentia
4.5". quæ prius erat inventa.
peracta, proveniet parallaxis supperior E C G,
0.54'.13". inferior verò K D L 4.59'.13". quæ si ab
invicem subtrahantur, manebit earum dif(sic)erentia
4.5". quæ prius erat inventa.
(100)
Problema XX.
Parallaxes phænomeni non polaris inquirere.
EXistente phænomeno cum duabus stellis fixis in eodem verticali, & acceptis eo momento apparentibus phænomeni ab utrâque fixarum distantiis. Ac rursus in secunda observatione, non habita ratione verticalium, acceptis distantiis phænomeni ab iisdem fixis, unà cum altitudine phænomeni & alterutrius fixarum. dico parallaxes utrique tempori congruas, notas reddi.
Sit Meridianus A B C, vertex B. Horizon A M
C, Polus mundi D. verticalis primæ observationis
 B H N, in quo duæ stellæ fixæ sint, H superior, G
inferior. Locus verus Phænomeni F, apparens E,
sint v. dictæ stellæ cū phænomeno motu primi mobilis
traductæ in locū alium : in quo talem situm in
cœlo tenebunt, qualem in adjecto Schemate vides.
Stellæ & Phænomenon iisdem literis in arcu circuli
magni notatæ sunt : in quo repræsentantur
B H N, in quo duæ stellæ fixæ sint, H superior, G
inferior. Locus verus Phænomeni F, apparens E,
sint v. dictæ stellæ cū phænomeno motu primi mobilis
traductæ in locū alium : in quo talem situm in
cœlo tenebunt, qualem in adjecto Schemate vides.
Stellæ & Phænomenon iisdem literis in arcu circuli
magni notatæ sunt : in quo repræsentantur
(101)
distantiæ phænomeni à stellis fixis, quomodo fuerint in prima observatione, in secunda v. observatione repræsentantur per arcus K G & K H. Nam K est locus phænomeni apparens secundæ observationis, verus F, in verticali B F M. Alius verticalis per stellam G ductus est B G L. Quoniam E G, E H, ex hypothesi primæ, & K G, K H, secundæ observationis nota sunt, erit triangulum, K G H, notorum laterum, unde notificantur etiam angulis(?) præcipuè v. anguli G H K, & G K H. Rursus in triangulo E H K, duo latera ex hypothesi, E H, H K, cum abg, E H K ab his conphenso, nota sunt ; ergò innotescent & reliqui anguli E K H & H E K. Tertio habemus triangulum K B G, cujus omnia tria latera cognita sunt. Nam K B est dist Phænomeni à vertice secundæ observationis, G B autem est distantia stellæ G à vertice, K G est distan. Phænomeni à stella. ergò per 4. ax. Sph. notus euadet angulus B K G, qui additus angulo G K H, efficiet totum F K H cognitum, qui rursus ablatus de angulo (in primo triangulo) E K H, relinquet angulum E K F. Postremum triangul. E F K, in quo notum est latus E K, cum binis angulis adiacentibus, innotescent igitur parallaxes utriusque temporis, E F quidem parallaxis primæ, K F autem secundæ observationis. Quod faciendum erat.
Problema XXI.
Tabulam Refractionum Solis construere.
NUnc tabulæ quædam sunt huic operi subnectendæ, quarum adminiculo tota ferè praxis
(102)
astronomica absolvitur, quæ quidem omnes universales sunt, & in quavis elevatione poli adhiberi possunt ; præter tabulam Refractionum, quæ ubique eadem retineri non potest, quia refractiones ipsæ, ob vaporum è terra surgentium varietatem, diversis in Locis variant. Ideoque quilibt practicus tabulam refractionum, suo loco convenientem sibi construere necessum habet, quod hoc modo fieri potest : Sole existente in ipso solstitio æstivo (quia tunc insensibilis est declinationis variatio) Cœlo satis serno, observetur quadrante azimuthali altitudo Solis, ad quemlibet gradum circulo verticali, & simul ad singulos gradus notentur quàm diligentissimè singula azimutha ipsis competentia incipiendo ab ipso ortus puncto, usque ad meridiem, & inde usque ad occasum. quo facto, tabulam conficere non erit difficile.

In apposito Schemate sit A B C D meridianus, B polus Horizontis, C polus mundi, A E D Horizon, E F, altitudo Solis vera, E G, apparens. In triangulo itaque B C F, cognita sunt duo latera,
(103)
B C, distantia polorum, & C F compl. maximæ declinationis Solis, (hanc enim primò cognitam habere necessum est) & angulus C B F, compl. scil. azimuthi per instrumentum observari ad 180. His cognitis facile innotescet latus B F, compl. altit. veræ. Si ergò altitudo vera E F, per calculum sic inventa, subtrahatur ab altit. E G per instrumentum observata, remanebit refractio Solis F G quæsita, & sic in quolibet altitudinis gradu est procedendum. Memineris tamen semper altitudinem Solis per observationem inventam, parallaxium additione esse corrigendam.
Aliter.
Potest etiam hæc tabula alio, eoque (ut mihi videtur) faciliori ac certiori construi modo, si in primis conficiatur tabula quædam, quæ ad singulos altitudinis gradus adscripta habeat competentia azimutha. Quomodo autem talis tabula sit construenda, facile ex præcedenti Schem. patet. Anm in triangulo B C F, omnia latera sunt cognita, B C, dist. polorū, C F, compl. maximæ decl. Solis, deinde B E, B F, B G, vel quicunque gradus altitudinis assumatur, per omnes enim gradus totius quadrantis est continuandum. Tribus itaque lateribus cognitis, invenitur angulus C B G, compl. azimuth quæsiti. Hac tabula constructa, quàm facillimè tabulam refractionis componere licet. Nam instrumentum ad quodlibet azimuth in tabula notatum ordine est firmandum, & cum Sol ad tale azimuth pervenerit, observanda tantum est ejus altitudo, quæ (parallaxium additione correcta) quantum altitudinem veram excedat, statim apparebit, idque est refractio quæsita.
(104)
Nec alia ratione construenda est tabula refract. Stellarum, idque tempore hyemali, cum longiores sunt noctes, & assumi potest stella quæcunque pro lubitu, dummodo ejus declinatio constet. Neque hic habenda est parallaxium ratio, stellæ enim fixæ nullam parallaxim admittunt.
Refractiones Lune quia quā proximè conveniunt cum refractionibus Solis (quod se crebrâ experientiâ invenisse testatur Tycho Brahe) & rationem tabulam refract. Lunarium conficiendi determinare sit quàm difficillium, propter subita declinationis variationem, itaque in observationibus Lunæ tabula refract. Solis commodè adhiberi potest. Reliquorum verò planetarum refractiones conveniunt cum refractionibus stellarum fixarum.
Placet jam hic apponere tabulam Refractionum Solis, Lunæ & stellarum, quam construxit, & in suis observationibus usus est Tycho Brahe Uraniburgi, cujus Latitudo sive Elevatio Poli est 55.54'.
Sequentes
TABULÆ
Occupanti in praxi Astronomica
maximè inserviunt.
Quæ sunt:
- 1. Tabula Refractionum.
- 2. Tab. Parallax(?).
- 3. Tab. Declin. Eclipt.
- 4. Tab. Ascen. Rectarum.
- 5. Distantiæ nonnullarum Stell.
- 6. Canon conversionis gr. &c.
- 7. Tab. continiens 100 Stellarum selctarum ascen. Rectas, & Decl.
- 8. Tab. continens prædictarum Stellarum Longitudines & Latitudines
| Tabula Refractionum Triplex. | |||||||
|---|---|---|---|---|---|---|---|
| Refract. | Refract. | Refract. | Refract. | Refract. | |||
| Alt. | ☉ | ☽ | Stell. | Alt. | ☉ | ☽ | |
| G. | /.//. | /.//. | /.//. | G. | /.//. | /.//. | |
| 0 | 34. 0 | 33. 0 | 30. 0 | 23 | 3.10 | 4.10 | |
| 1 | 26. 0 | 25. 0 | 21.30 | 24 | 2.50 | 3.45 | |
| 2 | 20. 0 | 20. 0 | 15.30 | 25 | 2.30 | 3.20 | |
| 3 | 17. 0 | 17. 0 | 12.30 | 26 | 2.15 | 3. 0 | |
| 4 | 15.30 | 15.20 | 11. 0 | 27 | 2. 0 | 2.40 | |
| 5 | 14.30 | 14.20 | 10. 0 | 28 | 1.45 | 2.20 | |
| 6 | 13.30 | 13.50 | 9. 0 | 29 | 1.35 | 2. 0 | |
| 7 | 12.45 | 12.45 | 8.15 | 30 | 1.25 | 1.40 | |
| 8 | 11.15 | 12. 0 | 6.45 | 31 | 1.15 | 1.30 | |
| 9 | 10.30 | 11.20 | 6. 0 | 32 | 1. 5 | 1.20 | |
| 10 | 10. 0 | 10.45 | 5.30 | 33 | 0.55 | 1.10 | |
| 11 | 9.30 | 10.10 | 5. 0 | 34 | 0.45 | 1. 0 | |
| 12 | 9. 0 | 9.35 | 4.30 | 35 | 0.35 | 0.5 | |
| 13 | 8.30 | 9. 0 | 4. 0 | 36 | 0.30 | 0.45 | |
| 14 | 8. 0 | 8.30 | 3.30 | 37 | 0.25 | 0.40 | |
| 15 | 7.30 | 8. 0 | 3. 0 | 38 | 0.20 | 0.35 | |
| 16 | 7. 0 | 7.30 | 2.30 | 39 | 0.15 | 0.30 | |
| 17 | 6.30 | 7. 0 | 2. 0 | 40 | 0.10 | 0.25 | |
| 18 | 5.45 | 6.30 | 1.15 | 41 | 0. 9 | 0.20 | |
| 19 | 5. 0 | 6. 0 | 0.30 | 42 | 0. 8 | 0.15 | |
| 20 | 4.30 | 5.30 | 0. 0 | 43 | 0. 7 | 0.10 | |
| 21 | 4. 0 | 5. 0 | 0. 0 | 44 | 0. 6 | 0. 5 | |
| 22 | 3.30 | 4.35 | 0. 0 | 45 | 0. 5 | 0. 0 | |
| Tabula Parallaxium Solarium In Circulo Verticali ad triplicem ejus à terra remotionem. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| alt. | Max. | Med. | Min. | alt. | Max. | Med. | Min. | alt. | Max. | Med. | Min. |
| G | /.//. | /.//. | /.//. | G | /.//. | /.//. | /.//. | G | /.//. | /.//. | /.//. |
| 0 | 2,54 | 3, 0 | 3, 7 | 30 | 2,30 | 2,36 | 2,42 | 60 | 1,27 | 1,30 | 1,33 |
| 1 | 2,54 | 3, 0 | 3, 7 | 31 | 2,28 | 2,34 | 2,40 | 61 | 1,25 | 1,28 | 1,31 |
| 2 | 2,54 | 3, 0 | 3, 7 | 32 | 2,27 | 2,32 | 2,38 | 62 | 1,22 | 1,25 | 1,28 |
| 3 | 2,54 | 3, 0 | 3, 7 | 33 | 2,25 | 2,30 | 2,37 | 63 | 1,19 | 1,22 | 1,25 |
| 4 | 2,53 | 2,59 | 3, 6 | 34 | 2,23 | 2,29 | 2,35 | 64 | 1,16 | 1,19 | 1,22 |
| 5 | 2,53 | 2,59 | 3, 6 | 35 | 2,22 | 2,27 | 2,33 | 65 | 1,13 | 1,16 | 1,19 |
| 6 | 2,53 | 2,59 | 3, 6 | 36 | 2,20 | 2,25 | 2,31 | 66 | 1,10 | 1,14 | 1,17 |
| 7 | 2,52 | 2,58 | 3, 5 | 37 | 2,18 | 2,23 | 2,29 | 67 | 1, 8 | 1,11 | 1,14 |
| 8 | 2,52 | 2,58 | 3, 5 | 38 | 2,17 | 2,21 | 2,27 | 68 | 1, 5 | 1, 8 | 1,11 |
| 9 | 2,51 | 2,57 | 3, 4 | 39 | 2,15 | 2,19 | 2,25 | 69 | 1, 2 | 1, 5 | 1, 8 |
| 10 | 2,51 | 2,57 | 3, 4 | 40 | 2,13 | 2,18 | 2,23 | 70 | 0,59 | 1, 2 | 1, 5 |
| 11 | 2,50 | 2,56 | 3, 3 | 41 | 2,11 | 2,16 | 2,21 | 71 | 0,56 | 0,59 | 1, 2 |
| 12 | 2,50 | 2,56 | 3, 3 | 42 | 2, 9 | 2,14 | 2,19 | 72 | 0,53 | 0,56 | 0,59 |
| 13 | 2,49 | 2,55 | 3, 2 | 43 | 2, 7 | 2,12 | 2,17 | 73 | 0,50 | 0,53 | 0,56 |
| 14 | 2,48 | 2,54 | 3, 1 | 44 | 2, 5 | 2, 9 | 2,15 | 74 | 0,47 | 0,49 | 0,52 |
| 15 | 2,48 | 2,54 | 3, 0 | 45 | 2, 3 | 2, 7 | 2,12 | 75 | 0,45 | 0,46 | 0,48 |
| 16 | 2,47 | 3,53 | 2,59 | 46 | 2, 1 | 2, 5 | 2,10 | 76 | 0,42 | 0,43 | 0,45 |
| 17 | 2,46 | 2,52 | 2,58 | 47 | 1,59 | 2, 3 | 2, 8 | 77 | 0,39 | 0,40 | 0,41 |
| 18 | 2,46 | 2,51 | 2,58 | 48 | 1,57 | 2, 0 | 2, 5 | 78 | 0,36 | 0,37 | 0,38 |
| 19 | 2,45 | 2,50 | 2,57 | 49 | 1,55 | 1,58 | 2, 3 | 79 | 0,32 | 0,34 | 0,35 |
| 20 | 2,44 | 2,50 | 2,56 | 50 | 1,52 | 1,56 | 2, 0 | 80 | 0,30 | 0,31 | 0,32 |
| 21 | 2,43 | 2,49 | 2,55 | 51 | 1,50 | 1,54 | 1,58 | 81 | 0,27 | 0,28 | 0,29 |
| 22 | 2,42 | 2,48 | 2,53 | 52 | 1,47 | 1,51 | 1,55 | 82 | 0,24 | 0,25 | 0,25 |
| 23 | 2,41 | 2,46 | 2,52 | 53 | 1,45 | 1,48 | 1,52 | 83 | 0,21 | 0,21 | 0,22 |
| 24 | 2,40 | 2,45 | 2,50 | 54 | 1,43 | 1,46 | 1,50 | 84 | 0,18 | 0,18 | 0,19 |
| 25 | 2,38 | 2,44 | 2,49 | 55 | 1,40 | 1,43 | 1,47 | 85 | 0,15 | 0,15 | 0,16 |
| 26 | 2,37 | 2,43 | 2,47 | 56 | 1,38 | 1,41 | 1,45 | 86 | 0,12 | 0,12 | 0,13 |
| 27 | 2,35 | 2,41 | 2,45 | 57 | 1,35 | 1,39 | 1,42 | 87 | 0, 9 | 0, 9 | 0, 9 |
| 28 | 2,33 | 2,39 | 2,41 | 58 | 1,32 | 1,36 | 1,39 | 88 | 0, 6 | 0, 6 | 0, 6 |
| 29 | 2,31 | 2,37 | 2,43 | 59 | 1,30 | 1,33 | 1,36 | 89 | 0, 3 | 0, 3 | 0, 3 |
| 30 | 2,30 | 2,36 | 2,42 | 60 | 1,27 | 1,30 | 1,33 | 90 | 0, 0 | 0, 0 | 0, 0 |
| Tabula Declinationis. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 0 | 0 | 00.00.00 | 11.30.43 | 20.13.22 | 0 | 30 | |||
| 10 | 00.04.00 | 04.00 | 11.34.15 | 03.32 | 20.15.29 | 02.07 | 50 | ||
| 20 | 00.07.59 | 03.59 | 11.37.46 | 03.31 | 20.17.36 | 02.07 | 40 | ||
| 30 | 00.11.58 | 03.59 | 11.41.17 | 03.31 | 20.19.42 | 02.06 | 30 | ||
| 40 | 00.15.57 | 03.59 | 11.44.48 | 03.31 | 20.21.47 | 02.05 | 20 | ||
| 50 | 00.19.56 | 03.59 | 11.48.18 | 03.30 | 20.23.52 | 02.05 | 10 | ||
| 1 | 0 | 00.23.56 | 04.00 | 11.51.48 | 03.30 | 20.25.57 | 02.05 | 0 | 29 |
| 10 | 00.27.55 | 03.59 | 11.55.17 | 03.29 | 20.28.01 | 02.04 | 50 | ||
| 20 | 00.31.55 | 04.00 | 11.58.46 | 03.29 | 20.30.04 | 02.03 | 40 | ||
| 30 | 00.35.55 | 04.00 | 12.02.15 | 03.29 | 20.32.06 | 02.02 | 30 | ||
| 40 | 00.39.54 | 03.59 | 12.05.44 | 03.29 | 20.34.07 | 02.01 | 20 | ||
| 50 | 00.43.53 | 03.59 | 12.09.12 | 03.28 | 20.36.08 | 02.01 | 10 | ||
| 2 | 0 | 00.47.53 | 04.00 | 12.12.40 | 03.28 | 20.38.09 | 02.01 | 0 | 28 |
| 10 | 00.51.12 | 03.19 | 12.16.08 | 03.28 | 20.40.09 | 02.00 | 50 | ||
| 20 | 00.55.52 | 04.40 | 12.19.35 | 03.27 | 20.42.08 | 01.59 | 40 | ||
| 30 | 00.59.51 | 03.59 | 12.23.02 | 03.27 | 20.44.06 | 01.58 | 30 | ||
| 40 | 01.03.50 | 03.59 | 12.26.29 | 03.27 | 20.46.04 | 01.58 | 20 | ||
| 50 | 01.07.49 | 03.59 | 12.29.55 | 03.26 | 20.48.01 | 01.57 | 10 | ||
| 3 | 0 | 01.11.49 | 04.00 | 12.33.21 | 03.26 | 20.49.58 | 01.57 | 0 | 27 |
| 10 | 01.15.48 | 03.59 | 12.36.46 | 03.25 | 20.51.54 | 01.56 | 50 | ||
| 20 | 01.19.47 | 03.59 | 12.40.12 | 03.26 | 20.53.59 | 02.05 | 40 | ||
| 30 | 01.23.46 | 03.59 | 12.43.37 | 03.25 | 20.55.44 | 01.45 | 30 | ||
| 40 | 01.27.45 | 03.59 | 12.47.01 | 03.24 | 20.57.38 | 01.54 | 20 | ||
| 50 | 01.31.44 | 03.59 | 12.50.25 | 03.24 | 20.59.32 | 01.54 | 10 | ||
| 4 | 0 | 01.35.43 | 03.59 | 12.53.49 | 03.24 | 21.01.25 | 01.53 | 0 | 26 |
| 10 | 01.39.42 | 03.59 | 12.57.12 | 03.23 | 21.03.17 | 01.52 | 50 | ||
| 20 | 01.43.41 | 03.59 | 14.00.35 | 03.23 | 21.05.09 | 01.52 | 40 | ||
| 30 | 01.47.40 | 03.59 | 13.03.58 | 03.23 | 21.07.00 | 01.51 | 30 | ||
| 40 | 01.51.39 | 03.59 | 13.07.21 | 03.23 | 21.08.50 | 01.50 | 20 | ||
| 50 | 01.55.38 | 03.59 | 13.10.43 | 03.22 | 21.10.40 | 01.50 | 10 | ||
| 5 | 0 | 01.59.37 | 03.59 | 13.14.05 | 03.22 | 21.12.29 | 01.49 | 0 | 25 |
| ♓︎ ♍︎ | dif S | ♒︎ ♌︎ | dif S | ♑︎ ♋︎ | dif S | ||||
| Eclipticæ. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 5 | 0 | 01.59.37 | 03.59 | 13.14.05 | 03.22 | 21.12.29 | 01.49 | 0 | 25 |
| 10 | 02.03.36 | 03.59 | 13.17.26 | 03.21 | 21.14.16 | 01.47 | 50 | ||
| 20 | 02.07.35 | 03.59 | 13.20.47 | 03.21 | 21.16.04 | 01.48 | 40 | ||
| 30 | 02.11.33 | 03.58 | 13.24.08 | 03.21 | 21.17.51 | 01.47 | 30 | ||
| 40 | 02.15.31 | 03.58 | 13.27.28 | 03.20 | 21.19.37 | 01.46 | 20 | ||
| 50 | 02.19.30 | 03.59 | 13.30.48 | 03.20 | 21.21.23 | 01.46 | 10 | ||
| 6 | 0 | 02.23.28 | 03.58 | 13.34.07 | 03.19 | 21.23.07 | 01.44 | 0 | 24 |
| 10 | 02.27.26 | 03.58 | 13.37.20 | 03.13 | 21.24.52 | 01.45 | 50 | ||
| 20 | 02.31.24 | 03.58 | 13.40.45 | 03.25 | 21.26.36 | 01.44 | 40 | ||
| 30 | 02.35.22 | 03.58 | 13.44.04 | 03.19 | 21.28.18 | 01.42 | 30 | ||
| 40 | 02.39.20 | 03.58 | 13.47.22 | 03.18 | 21.30.00 | 01.42 | 20 | ||
| 50 | 02.43.18 | 03.58 | 13.50.40 | 03.18 | 21.31.42 | 01.42 | 10 | ||
| 7 | 0 | 02.47.16 | 03.58 | 13.53.57 | 03.17 | 21.33.22 | 01.40 | 0 | 23 |
| 10 | 02.51.14 | 03.58 | 13.57.14 | 03.17 | 21.35.02 | 01.40 | 50 | ||
| 20 | 02.55.12 | 03.58 | 14.00.30 | 03.16 | 21.36.43 | 01.41 | 40 | ||
| 30 | 02.59.10 | 03.58 | 14.03.46 | 03.16 | 21.38.22 | 01.39 | 30 | ||
| 40 | 03.03.08 | 03.58 | 14.07.02 | 03.16 | 21.40.00 | 01.38 | 20 | ||
| 50 | 03.07.06 | 03.58 | 14.10.17 | 03.15 | 21.41.38 | 01.38 | 10 | ||
| 8 | 0 | 03.11.04 | 03.58 | 14.13.32 | 03.15 | 21.43.15 | 01.37 | 0 | 22 |
| 10 | 03.15.02 | 03.58 | 14.16.46 | 03.14 | 21.44.51 | 01.36 | 50 | ||
| 20 | 03.18.59 | 03.57 | 14.20.00 | 03.14 | 21.46.26 | 01.35 | 40 | ||
| 30 | 03.22.56 | 03.57 | 14.23.14 | 03.14 | 21.48.01 | 01.35 | 30 | ||
| 40 | 03.26.53 | 03.57 | 14.26.27 | 03.13 | 21.49.35 | 01.34 | 20 | ||
| 50 | 03.30.50 | 03.57 | 14.29.40 | 03.13 | 21.51.09 | 01.34 | 10 | ||
| 9 | 0 | 03.34.47 | 03.57 | 14.32.53 | 03.13 | 21.52.42 | 01.33 | 0 | 21 |
| 10 | 03.38.44 | 03.57 | 14.36.05 | 03.12 | 21.54.14 | 01.32 | 50 | ||
| 20 | 03.42.41 | 03.57 | 14.39.17 | 03.12 | 21.55.45 | 01.31 | 40 | ||
| 30 | 03.46.38 | 03.57 | 14.42.28 | 03.11 | 21.57.16 | 01.31 | 30 | ||
| 40 | 03.50.35 | 03.57 | 14.45.39 | 03.11 | 21.58.46 | 01.30 | 20 | ||
| 50 | 03.54.32 | 03.57 | 14.48.49 | 03.10 | 21.00.16 | 01.30 | 10 | ||
| 10 | 0 | 03.58.28 | 03.56 | 14.51.59 | 03.10 | 21.01.45 | 01.29 | 0 | 20 |
| ♓︎ ♍︎ | dif S | ♒︎ ♌︎ | dif S | ♑︎ ♋︎ | dif S | ||||
| Ad Gradum dena | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 10 | 0 | 03.58.28 | 03.56 | 14.51.59 | 03.10 | 21.01.45 | 01.29 | 0 | 20 |
| 10 | 04.02.24 | 03.56 | 14.55.09 | 03.10 | 22.03.13 | 01.28 | 50 | ||
| 20 | 04.06.20 | 03.56 | 14.58.18 | 03.09 | 22.04.40 | 01.27 | 40 | ||
| 30 | 04.10.16 | 03.56 | 15.01.27 | 03.09 | 22.06.06 | 01.26 | 30 | ||
| 40 | 04.14.12 | 03.56 | 15.04.43 | 03.16 | 22.07.32 | 01.26 | 20 | ||
| 50 | 04.18.08 | 03.56 | 15.07.35 | 02.52 | 22.08.57 | 01.25 | 10 | ||
| 11 | 0 | 04.22.04 | 03.56 | 15.10.50 | 03.15 | 22.10.22 | 01.25 | 0 | 19 |
| 10 | 04.26.00 | 03.56 | 15.30.57 | 20.07 | 22.11.46 | 01.24 | 50 | ||
| 20 | 04.29.56 | 03.56 | 15.17.04 | 46.07 | 22.13.09 | 01.23 | 40 | ||
| 30 | 04.33.52 | 03.56 | 15.20.10 | 03.06 | 22.14.32 | 01.23 | 30 | ||
| 40 | 04.37.47 | 03.55 | 15.23.16 | 03.06 | 22.15.54 | 01.22 | 20 | ||
| 50 | 04.41.42 | 03.55 | 15.26.21 | 03.05 | 22.17.15 | 01.21 | 10 | ||
| 12 | 0 | 04.45.37 | 03.55 | 15.29.26 | 03.05 | 22.18.35 | 01.20 | 0 | 18 |
| 10 | 04.49.32 | 03.55 | 15.32.31 | 03.05 | 22.19.54 | 01.19 | 50 | ||
| 20 | 04.53.27 | 03.55 | 15.35.35 | 03.04 | 22.21.13 | 01.19 | 40 | ||
| 30 | 04.57.22 | 03.55 | 15.38.39 | 03.04 | 22.22.31 | 01.18 | 30 | ||
| 40 | 05.01.17 | 03.55 | 15.41.42 | 03.03 | 22.23.49 | 01.18 | 20 | ||
| 50 | 05.05.11 | 03.54 | 15.44.45 | 03.03 | 22.25.06 | 01.17 | 10 | ||
| 13 | 0 | 05.09.05 | 03.54 | 15.47.47 | 03.02 | 22.26.22 | 01.16 | 0 | 17 |
| 10 | 05.12.59 | 03.54 | 15.50.49 | 03.02 | 22.27.37 | 01.15 | 50 | ||
| 20 | 05.16.53 | 03.54 | 15.53.50 | 03.01 | 22.28.52 | 01.15 | 40 | ||
| 30 | 05.20.47 | 03.54 | 15.56.51 | 03.01 | 22.30.06 | 01.14 | 30 | ||
| 40 | 05.24.41 | 03.54 | 15.59.51 | 03.00 | 22.31.19 | 01.13 | 20 | ||
| 50 | 05.28.35 | 03.54 | 16.02.51 | 03.00 | 22.32.32 | 01.13 | 10 | ||
| 14 | 0 | 05.32.29 | 03.54 | 16.05.51 | 03.00 | 22.33.44 | 01.12 | 0 | 16 |
| 10 | 05.36.22 | 03.53 | 16.08.50 | 02.59 | 22.34.55 | 01.11 | 50 | ||
| 20 | 05.40.15 | 03.53 | 16.11.49 | 02.59 | 22.36.03 | 01.08 | 40 | ||
| 30 | 05.44.08 | 03.53 | 16.14.47 | 02.58 | 22.37.14 | 01.11 | 30 | ||
| 40 | 05.48.01 | 03.53 | 16.17.45 | 02.58 | 22.38.23 | 01.09 | 20 | ||
| 50 | 05.51.54 | 03.53 | 16.20.42 | 02.57 | 22.39.31 | 01.08 | 10 | ||
| 15 | 0 | 05.55.46 | 03.52 | 16.23.39 | 02.57 | 22.40.39 | 01.08 | 0 | 15 |
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| Scrapula extensa. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 15 | 0 | 05.55.46 | 03.52 | 16.23.39 | 02.57 | 22.40.39 | 01.08 | 0 | 15 |
| 10 | 05.59.38 | 03.52 | 16.26.34 | 02.55 | 22.41.47 | 01.08 | 50 | ||
| 20 | 06.03.30 | 03.52 | 16.29.30 | 02.56 | 22.42.53 | 01.06 | 40 | ||
| 30 | 06.07.22 | 03.52 | 16.32.25 | 02.55 | 22.43.58 | 01.05 | 30 | ||
| 40 | 06.11.14 | 03.52 | 16.35.20 | 02.55 | 22.45.03 | 01.05 | 20 | ||
| 50 | 06.15.06 | 03.52 | 16.38.15 | 02.55 | 22.46.07 | 01.04 | 10 | ||
| 16 | 0 | 06.18.58 | 03.52 | 16.41.09 | 02.54 | 22.47.10 | 01.03 | 0 | 14 |
| 10 | 06.22.50 | 03.52 | 16.44.02 | 02.53 | 22.48.12 | 01.02 | 50 | ||
| 20 | 06.26.42 | 03.52 | 16.46.55 | 02.53 | 22.49.14 | 01.02 | 40 | ||
| 30 | 06.30.33 | 03.51 | 16.49.48 | 02.53 | 22.50.15 | 01.01 | 30 | ||
| 40 | 06.34.24 | 03.51 | 16.52.40 | 02.52 | 22.51.15 | 01.00 | 20 | ||
| 50 | 06.38.15 | 03.51 | 16.55.31 | 02.51 | 22.52.14 | 00.59 | 10 | ||
| 17 | 0 | 06.42.06 | 03.51 | 16.58.22 | 02.51 | 22.53.13 | 00.59 | 0 | 13 |
| 10 | 06.45.56 | 03.50 | 17.01.13 | 02.51 | 22.54.11 | 00.58 | 50 | ||
| 20 | 06.49.46 | 03.50 | 17.04.03 | 02.50 | 22.55.09 | 00.58 | 40 | ||
| 30 | 06.53.36 | 03.50 | 17.06.52 | 02.49 | 22.56.06 | 00.57 | 30 | ||
| 40 | 06.57.26 | 03.50 | 17.09.41 | 02.49 | 22.57.02 | 00.56 | 20 | ||
| 50 | 07.01.16 | 03.50 | 17.12.30 | 02.49 | 22.57.57 | 00.55 | 10 | ||
| 18 | 0 | 07.05.06 | 03.50 | 17.15.18 | 02.48 | 22.58.51 | 00.54 | 0 | 12 |
| 10 | 07.08.55 | 03.49 | 17.18.05 | 02.47 | 22.59.45 | 00.54 | 50 | ||
| 20 | 07.12.44 | 03.49 | 17.20.52 | 02.47 | 23.00.38 | 00.53 | 40 | ||
| 30 | 07.16.33 | 03.49 | 17.21.38 | 00.46 | 23.01.31 | 00.53 | 30 | ||
| 40 | 07.20.22 | 03.49 | 17.26.24 | 04.46 | 23.02.22 | 00.51 | 20 | ||
| 50 | 07.24.11 | 03.49 | 17.29.09 | 02.45 | 23.03.13 | 00.51 | 10 | ||
| 19 | 0 | 07.28.00 | 03.49 | 17.31.54 | 02.45 | 23.04.03 | 00.50 | 0 | 11 |
| 10 | 07.31.48 | 03.48 | 17.34.39 | 02.45 | 23.04.52 | 00.49 | 50 | ||
| 20 | 07.35.36 | 03.48 | 17.37.23 | 02.44 | 23.05.41 | 00.49 | 40 | ||
| 30 | 07.39.24 | 03.48 | 17.40.07 | 02.44 | 23.06.29 | 00.48 | 30 | ||
| 40 | 07.43.12 | 03.48 | 17.42.50 | 02.43 | 23.07.16 | 00.47 | 20 | ||
| 50 | 07.46.59 | 03.47 | 17.45.32 | 02.42 | 23.08.02 | 00.46 | 10 | ||
| 20 | 0 | 07.50.46 | 03.47 | 17.48.14 | 02.42 | 23.08.47 | 00.45 | 0 | 10 |
| ♓︎ ♍︎ | dif S | ♒︎ ♌︎ | dif S | ♑︎ ♋︎ | dif S | ||||
| (?)uxta maximam Declinat. Solis | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 20 | 0 | 07.50.46 | 03.47 | 17.48.14 | 02.42 | 23.08.47 | 00.45 | 0 | 10 |
| 10 | 07.54.33 | 03.47 | 17.50.55 | 02.41 | 23.09.32 | 00.45 | 50 | ||
| 20 | 07.58.20 | 03.47 | 17.53.36 | 02.41 | 23.10.16 | 00.44 | 40 | ||
| 30 | 08.02.07 | 03.47 | 17.56.16 | 02.40 | 23.10.59 | 00.43 | 30 | ||
| 40 | 08.05.54 | 03.47 | 17.58.56 | 02.40 | 23.11.42 | 00.43 | 20 | ||
| 50 | 08.09.40 | 03.46 | 18.01.35 | 02.39 | 23.12.24 | 00.42 | 10 | ||
| 21 | 0 | 08.13.26 | 03.46 | 18.04.14 | 02.39 | 23.13.05 | 00.41 | 0 | 9 |
| 10 | 08.17.12 | 03.46 | 18.06.52 | 02.38 | 23.13.45 | 00.40 | 50 | ||
| 20 | 08.20.58 | 03.46 | 18.09.30 | 02.38 | 23.14.24 | 00.39 | 40 | ||
| 30 | 08.24.43 | 03.45 | 18.12.08 | 02.38 | 23.15.03 | 00.39 | 30 | ||
| 40 | 08.28.28 | 03.45 | 18.14.45 | 02.37 | 23.15.41 | 00.38 | 20 | ||
| 50 | 08.32.13 | 03.45 | 18.17.21 | 02.36 | 23.16.19 | 00.38 | 10 | ||
| 22 | 0 | 08.35.58 | 03.45 | 18.19.57 | 02.36 | 23.16.56 | 00.37 | 0 | 8 |
| 10 | 08.39.42 | 03.44 | 18.22.32 | 02.35 | 23.17.32 | 00.36 | 50 | ||
| 20 | 08.43.26 | 03.44 | 18.25.06 | 02.34 | 23.18.07 | 00.35 | 40 | ||
| 30 | 08.47.10 | 03.44 | 18.27.40 | 02.34 | 23.18.41 | 00.34 | 30 | ||
| 40 | 08.50.54 | 03.44 | 18.30.13 | 02.33 | 23.19.15 | 00.34 | 20 | ||
| 50 | 08.54.37 | 03.43 | 18.32.46 | 02.33 | 23.19.48 | 00.33 | 10 | ||
| 23 | 0 | 08.58.20 | 03.43 | 18.35.18 | 02.32 | 23.20.20 | 00.32 | 0 | 7 |
| 10 | 09.02.03 | 03.43 | 18.37.50 | 02.32 | 23.20.52 | 00.32 | 50 | ||
| 20 | 09.05.46 | 03.43 | 18.40.21 | 02.31 | 23.21.23 | 00.31 | 40 | ||
| 30 | 09.09.28 | 03.42 | 18.42.52 | 02.31 | 23.21.53 | 00.30 | 30 | ||
| 40 | 09.13.10 | 03.42 | 18.45.22 | 02.30 | 23.22.22 | 00.29 | 20 | ||
| 50 | 09.16.52 | 03.42 | 18.47.52 | 02.30 | 23.22.50 | 00.28 | 10 | ||
| 24 | 0 | 09.20.34 | 03.42 | 18.50.21 | 02.29 | 23.23.18 | 00.28 | 0 | 6 |
| 10 | 09.24.16 | 03.42 | 18.52.50 | 02.29 | 23.23.45 | 00.27 | 50 | ||
| 20 | 09.27.58 | 03.42 | 18.55.18 | 02.28 | 23.24.11 | 00.26 | 40 | ||
| 30 | 09.31.39 | 03.41 | 18.57.45 | 02.27 | 23.24.36 | 00.25 | 30 | ||
| 40 | 09.35.20 | 03.41 | 19.00.12 | 02.27 | 23.25.01 | 00.25 | 20 | ||
| 50 | 09.39.01 | 03.41 | 19.02.38 | 02.26 | 23.25.25 | 00.24 | 10 | ||
| 25 | 0 | 09.42.41 | 03.40 | 19.05.04 | 02.26 | 23.25.48 | 00.23 | 0 | 5 |
| ♓︎ ♍︎ | dif S | ♒︎ ♌︎ | dif S | ♑︎ ♋︎ | dif S | ||||
| Hujus seculi 23.31'.30". | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ♈︎ ♎︎ | dif A | ♉︎ ♏︎ | dif A | ♊︎ ♐︎ | dif A | ||||
| G | M | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. | M | G |
| 25 | 0 | 09.42.41 | 03.40 | 19.05.04 | 02.26 | 23.25.48 | 00.23 | 0 | 5 |
| 10 | 09.46.21 | 03.40 | 19.07.29 | 02.25 | 23.26.10 | 00.22 | 50 | ||
| 20 | 09.50.01 | 03.40 | 19.09.54 | 02.25 | 23.26.31 | 00.21 | 40 | ||
| 30 | 09.53.41 | 03.40 | 19.12.18 | 02.24 | 23.26.52 | 00.21 | 30 | ||
| 40 | 09.57.20 | 03.39 | 19.14.41 | 02.23 | 23.27.12 | 00.20 | 20 | ||
| 50 | 10.00.59 | 03.39 | 19.17.04 | 02.23 | 23.27.32 | 00.20 | 10 | ||
| 26 | 0 | 10.04.38 | 03.39 | 19.19.26 | 02.22 | 23.27.51 | 00.19 | 0 | 4 |
| 10 | 10.08.16 | 03.38 | 19.21.48 | 02.22 | 23.28.09 | 00.18 | 50 | ||
| 20 | 10.11.54 | 03.38 | 19.24.09 | 02.21 | 23.28.26 | 00.17 | 40 | ||
| 30 | 10.15.32 | 03.38 | 19.26.29 | 02.20 | 23.28.42 | 00.16 | 30 | ||
| 40 | 10.19.10 | 03.38 | 19.28.49 | 02.20 | 23.28.58 | 00.16 | 20 | ||
| 50 | 10.22.47 | 03.37 | 19.31.08 | 02.19 | 23.29.13 | 00.15 | 10 | ||
| 27 | 0 | 10.26.24 | 03.37 | 19.33.27 | 02.19 | 23.29.27 | 00.14 | 0 | 3 |
| 10 | 10.30.01 | 03.37 | 19.35.45 | 02.18 | 23.29.40 | 00.13 | 50 | ||
| 20 | 10.33.38 | 03.37 | 19.38.03 | 02.18 | 23.29.52 | 00.12 | 40 | ||
| 30 | 10.37.14 | 03.36 | 19.40.20 | 02.17 | 23.30.04 | 00.12 | 30 | ||
| 40 | 10.40.50 | 03.36 | 19.42.36 | 02.16 | 23.30.15 | 00.11 | 20 | ||
| 50 | 10.44.26 | 03.36 | 19.44.52 | 02.16 | 23.30.25 | 00.10 | 10 | ||
| 28 | 0 | 10.48.02 | 03.36 | 19.47.07 | 02.15 | 23.30.35 | 00.10 | 0 | 2 |
| 10 | 10.51.37 | 03.35 | 19.49.22 | 02.15 | 23.30.44 | 00.09 | 50 | ||
| 20 | 10.55.12 | 03.35 | 19.51.36 | 02.14 | 23.30.52 | 00.08 | 40 | ||
| 30 | 10.58.46 | 03.34 | 19.53.50 | 02.14 | 23.30.59 | 00.07 | 30 | ||
| 40 | 11.02.20 | 03.34 | 19.56.03 | 02.13 | 23.31.06 | 00.07 | 20 | ||
| 50 | 11.05.54 | 03.34 | 19.58.15 | 02.12 | 23.31.12 | 00.06 | 10 | ||
| 29 | 0 | 11.09.27 | 03.33 | 20.00.26 | 02.11 | 23.31.17 | 00.05 | 0 | 1 |
| 10 | 11.13.00 | 03.33 | 20.02.37 | 02.11 | 23.31.21 | 00.04 | 50 | ||
| 20 | 11.16.33 | 03.33 | 20.04.47 | 02.10 | 23.31.24 | 00.03 | 40 | ||
| 30 | 11.20.06 | 03.33 | 20.06.57 | 02.10 | 23.31.26 | 00.02 | 30 | ||
| 40 | 11.23.38 | 03.32 | 20.09.06 | 02.09 | 23.31.28 | 00.02 | 20 | ||
| 50 | 11.27.10 | 03.32 | 20.11.14 | 02.08 | 23.31.29 | 00.01 | 10 | ||
| 30 | 0 | 11.30.42 | 03.32 | 20.13.22 | 02.08 | 23.31.30 | 00.01 | 0 | 0 |
| ♓︎ ♍︎ | dif S | ♒︎ ♌︎ | dif S | ♑︎ ♋︎ | dif S | ||||
| Tabula Ascentionum rectarum | ||||||
|---|---|---|---|---|---|---|
| ♈︎ | Differ. | ♉︎ | Differ. | ♊︎ | Differ. | |
| G | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. |
| 0 | 00.00.00 | 27.53.43 | 57.48.07 | |||
| 1 | 00.55.01 | 55.01 | 28.51.05 | 57.22 | 58.50.40 | 62.33 |
| 2 | 01.50.02 | 55.01 | 29.48.36 | 57.31 | 59.53.23 | 62.43 |
| 3 | 02.45.04 | 55.02 | 30.46.16 | 57.40 | 60.56.16 | 62.53 |
| 4 | 03.40.07 | 55.03 | 31.44.05 | 57.49 | 61.59.19 | 63.03 |
| 5 | 04.35.11 | 55.04 | 32.42.03 | 57.58 | 63.02.32 | 63.13 |
| 6 | 05.30.17 | 55.06 | 33.40.11 | 58.08 | 64.05.55 | 63.23 |
| 7 | 06.25.25 | 55.08 | 34.38.29 | 58.18 | 65.09.27 | 63.32 |
| 8 | 07.20.35 | 55.10 | 35.36.57 | 58.28 | 66.13.08 | 63.41 |
| 9 | 08.15.47 | 55.12 | 36.35.35 | 58.38 | 67.16.57 | 63.49 |
| 10 | 09.11.02 | 55.15 | 37.34.23 | 58.48 | 68.20.54 | 63.57 |
| 11 | 10.06.20 | 55.18 | 38.33.22 | 58.59 | 69.24.59 | 64.05 |
| 12 | 11.01.41 | 55.21 | 39.32.32 | 59.10 | 70.29.12 | 64.13 |
| 13 | 11.57.06 | 55.25 | 40.31.52 | 59.20 | 71.33.32 | 64.20 |
| 14 | 12.52.35 | 55.29 | 41.31.22 | 59.30 | 72.37.59 | 64.27 |
| 15 | 13.48.09 | 55.34 | 42.31.03 | 59.41 | 73.42.33 | 64.34 |
| 16 | 14.43.48 | 55.39 | 43.30.55 | 59.52 | 74.47.13 | 64.40 |
| 17 | 15.39.32 | 55.44 | 44.30.58 | 60.03 | 75.51.59 | 64.46 |
| 18 | 16.35.21 | 55.49 | 45.31.11 | 60.13 | 76.56.51 | 64.52 |
| 19 | 17.31.16 | 55.55 | 46.31.36 | 60.25 | 78.01.47 | 64.56 |
| 20 | 18.27.17 | 56.01 | 47.32.12 | 60.36 | 79.00.48 | 59.01 |
| 21 | 19.23.24 | 56.07 | 48.32.59 | 60.47 | 80.15.54 | 75.06 |
| 22 | 20.19.37 | 56.13 | 49.33.57 | 60.58 | 81.17.04 | 61.10 |
| 23 | 21.15.57 | 56.20 | 50.35.06 | 61.09 | 82.22.18 | 65.14 |
| 24 | 22.12.24 | 56.27 | 51.36.25 | 61.19 | 83.27.35 | 65.17 |
| 25 | 23.08.58 | 56.34 | 52.37.55 | 61.30 | 84.32.55 | 65.20 |
| 26 | 24.05.39 | 56.41 | 53.39.36 | 61.41 | 85.38.18 | 65.23 |
| 27 | 25.02.28 | 56.49 | 54.41.28 | 61.52 | 86.43.42 | 65.24 |
| 28 | 25.59.25 | 56.57 | 55.43.31 | 62.03 | 87.49.07 | 65.25 |
| 29 | 26.56.30 | 57.05 | 56.45.44 | 62.13 | 88.54.33 | 65.26 |
| 30 | 27.53.43 | 57.13 | 57.48.07 | 62.23 | 90.00.00 | 65.27 |
| ad singulos Eclipticæ gradus | ||||||
|---|---|---|---|---|---|---|
| ♋︎ | Differ. | ♌︎ | Differ. | ♍︎ | Differ. | |
| G | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. |
| 0 | 90.00.00 | 122.11.35 | 152.06.18 | |||
| 1 | 91.05.27 | 65.27 | 123.14.16 | 62.41 | 153.03.31 | 57.13 |
| 2 | 92.10.53 | 65.26 | 124.16.29 | 62.13 | 154.00.36 | 57.05 |
| 3 | 93.16.18 | 65.25 | 125.18.32 | 62.03 | 154.57.33 | 56.57 |
| 4 | 94.21.42 | 65.24 | 126.20.24 | 61.52 | 155.54.22 | 56.49 |
| 5 | 95.27.05 | 65.23 | 127.22.05 | 61.41 | 156.51.03 | 56.41 |
| 6 | 96.32.25 | 65.20 | 128.23.35 | 61.30 | 157.47.37 | 56.34 |
| 7 | 97.37.42 | 65.17 | 129.24.54 | 61.19 | 158.44.04 | 56.27 |
| 8 | 98.42.56 | 65.14 | 130.26.03 | 61.09 | 159.40.23 | 56.19 |
| 9 | 99.48.06 | 65.10 | 131.27.01 | 60.58 | 160.36.36 | 56.13 |
| 10 | 100.53.12 | 65.06 | 132.27.48 | 60.47 | 161.32.43 | 56.07 |
| 11 | 101.58.13 | 65.01 | 133.28.24 | 60.36 | 162.28.44 | 56.01 |
| 12 | 103.03.09 | 64.56 | 134.28.49 | 60.25 | 163.24.39 | 55.55 |
| 13 | 104.08.01 | 64.52 | 135.29.02 | 60.13 | 164.20.28 | 55.49 |
| 14 | 105.12.47 | 64.46 | 136.29.05 | 60.03 | 165.16.12 | 55.44 |
| 15 | 106.17.27 | 64.40 | 137.28.57 | 59.52 | 166.11.51 | 55.39 |
| 16 | 107.22.01 | 64.34 | 138.28.38 | 59.41 | 167.07.25 | 55.34 |
| 17 | 108.26.28 | 64.27 | 139.28.08 | 59.30 | 168.02.54 | 55.29 |
| 18 | 109.30.48 | 64.20 | 140.27.28 | 59.20 | 168.58.19 | 55.25 |
| 19 | 110.35.01 | 64.13 | 141.26.38 | 59.10 | 169.53.40 | 55.21 |
| 20 | 111.39.06 | 64.05 | 142.24.37 | 57.59 | 170.48.58 | 55.18 |
| 21 | 112.43.04 | 63.58 | 143.24.25 | 59.48 | 171.44.13 | 55.15 |
| 22 | 113.46.53 | 63.49 | 144.23.03 | 58.38 | 172.39.25 | 55.12 |
| 23 | 114.50.34 | 63.41 | 145.21.31 | 58.28 | 173.34.35 | 55.10 |
| 24 | 115.54.06 | 63.32 | 146.19.49 | 58.18 | 174.29.43 | 55.08 |
| 25 | 116.57.29 | 63.23 | 147.17.57 | 58.08 | 175.24.49 | 55.06 |
| 26 | 118.00.42 | 63.13 | 148.15.55 | 57.58 | 176.19.53 | 55.04 |
| 27 | 119.03.45 | 63.03 | 149.13.44 | 57.49 | 177.14.56 | 55.03 |
| 28 | 120.06.38 | 62.53 | 150.11.24 | 57.40 | 178.09.58 | 55.02 |
| 29 | 121.09.20 | 62.42 | 151.08.55 | 57.31 | 179.04.59 | 55.01 |
| 30 | 122.11.53 | 62.33 | 152.06.18 | 57.23 | 180.00.00 | 55.01 |
| Præsupponens Declin. Maximam | ||||||
|---|---|---|---|---|---|---|
| ♎︎ | Differ.> | ♏︎ | Differ. | ♐︎ | Differ. | |
| G | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. |
| 0 | 180.00.00 | 207.53.43 | 237.48.07 | |||
| 1 | 180.55.01 | 55.01 | 208.51.05 | 57.22 | 238.50.40 | 62.33 |
| 2 | 181.50.02 | 55.01 | 209.48.36 | 57.31 | 239.53.23 | 62.43 |
| 3 | 182.45.04 | 55.02 | 210.46.16 | 57.40 | 240.56.16 | 62.53 |
| 4 | 183.40.07 | 55.03 | 211.44.05 | 57.49 | 241.59.19 | 63.03 |
| 5 | 184.35.11 | 55.04 | 212.42.03 | 57.58 | 243.02.32 | 63.13 |
| 6 | 185.30.17 | 55.06 | 213.40.11 | 58.08 | 244.05.55 | 63.23 |
| 7 | 186.25.25 | 55.08 | 214.38.29 | 58.18 | 245.09.27 | 63.32 |
| 8 | 187.20.35 | 55.10 | 215.36.57 | 58.28 | 246.13.08 | 63.41 |
| 9 | 188.15.47 | 55.12 | 216.35.35 | 58.38 | 247.16.57 | 63.49 |
| 10 | 189.11.02 | 55.15 | 217.34.23 | 58.48 | 248.20.54 | 63.57 |
| 11 | 190.06.20 | 55.18 | 218.33.22 | 58.59 | 249.24.59 | 64.05 |
| 12 | 191.01.41 | 55.21 | 219.32.32 | 59.10 | 250.29.12 | 64.13 |
| 13 | 191.57.06 | 55.25 | 220.31.52 | 59.20 | 251.33.32 | 64.20 |
| 14 | 192.52.35 | 55.29 | 221.31.22 | 59.30 | 252.37.59 | 64.27 |
| 15 | 193.48.09 | 55.34 | 222.31.03 | 59.41 | 253.42.33 | 64.34 |
| 16 | 194.43.48 | 55.39 | 223.30.55 | 59.52 | 254.47.13 | 64.40 |
| 17 | 195.39.32 | 55.44 | 224.30.58 | 60.03 | 255.51.59 | 64.46 |
| 18 | 196.35.21 | 55.49 | 225.31.11 | 60.13 | 256.56.51 | 64.52 |
| 19 | 197.31.16 | 55.55 | 226.31.36 | 60.25 | 258.01.47 | 64.56 |
| 20 | 198.27.17 | 56.01 | 227.32.12 | 60.36 | 259.06.48 | 65.01 |
| 21 | 199.23.24 | 56.07 | 228.32.59 | 60.47 | 260.11.54 | 65.06 |
| 22 | 200.19.37 | 56.13 | 229.33.57 | 60.58 | 261.17.04 | 65.10 |
| 23 | 201.15.57 | 56.20 | 230.35.06 | 61.09 | 262.22.18 | 65.14 |
| 24 | 202.12.24 | 56.27 | 231.30.25 | 55.19 | 263.27.35 | 65.17 |
| 25 | 203.08.58 | 56.34 | 232.37.55 | 67.30 | 264.32.55 | 65.20 |
| 26 | 204.05.39 | 56.41 | 233.39.36 | 61.41 | 265.38.18 | 65.23 |
| 27 | 205.02.28 | 56.49 | 234.41.28 | 61.52 | 266.43.42 | 65.24 |
| 28 | 205.59.25 | 56.57 | 235.43.31 | 62.03 | 267.49.07 | 65.25 |
| 29 | 206.56.30 | 57.05 | 236.45.44 | 62.13 | 268.54.33 | 65.26 |
| 30 | 207.53.43 | 57.13 | 237.48.07 | 62.23 | 270.00.00 | 65.27 |
| Qua hoc ævo est 23.31'.30". | ||||||
|---|---|---|---|---|---|---|
| ♑︎ | Differ. | ♒︎ | Differ. | ♓︎ | Differ. | |
| G | o././/. | /.//. | o././/. | /.//. | o././/. | /.//. |
| 0 | 270.00.00 | 302.11.53 | 332.06.18 | |||
| 1 | 271.05.27 | 65.27 | 303.14.16 | 62.23 | 333.03.31 | 57.13 |
| 2 | 272.10.53 | 65.26 | 304.16.29 | 62.13 | 334.00.36 | 57.05 |
| 3 | 273.16.18 | 65.25 | 305.18.32 | 62.03 | 334.57.33 | 56.57 |
| 4 | 274.21.42 | 65.24 | 306.20.24 | 61.52 | 335.54.22 | 56.49 |
| 5 | 275.27.05 | 65.23 | 307.22.05 | 61.41 | 336.51.03 | 56.41 |
| 6 | 276.32.25 | 65.20 | 308.23.35 | 61.30 | 337.47.37 | 56.34 |
| 7 | 277.37.42 | 65.17 | 309.24.54 | 61.19 | 338.44.04 | 56.27 |
| 8 | 278.42.56 | 65.14 | 310.20.03 | 55.09 | 339.40.23 | 56.19 |
| 9 | 279.48.06 | 65.10 | 311.27.01 | 66.58 | 340.36.36 | 56.13 |
| 10 | 280.53.12 | 65.06 | 312.27.48 | 60.47 | 341.32.43 | 56.07 |
| 11 | 281.58.13 | 65.01 | 313.28.24 | 60.36 | 342.28.44 | 56.01 |
| 12 | 283.03.09 | 64.56 | 314.28.49 | 60.25 | 343.24.39 | 55.55 |
| 13 | 284.08.01 | 64.52 | 315.29.02 | 60.13 | 344.20.28 | 55.49 |
| 14 | 285.13.47 | 65.46 | 316.29.05 | 60.03 | 345.16.12 | 55.44 |
| 15 | 286.17.27 | 63.40 | 317.28.57 | 59.52 | 346.11.51 | 55.39 |
| 16 | 287.22.01 | 64.34 | 318.28.38 | 59.41 | 347.07.25 | 55.34 |
| 17 | 288.26.28 | 64.27 | 319.28.08 | 59.30 | 348.02.54 | 55.29 |
| 18 | 289.30.48 | 64.20 | 320.27.28 | 59.20 | 348.58.19 | 55.25 |
| 19 | 290.35.01 | 64.13 | 321.26.38 | 59.10 | 349.53.40 | 55.21 |
| 20 | 291.39.06 | 64.05 | 322.25.37 | 58.59 | 350.48.58 | 55.18 |
| 21 | 292.43.04 | 63.58 | 323.24.25 | 58.48 | 351.44.13 | 55.15 |
| 22 | 293.46.53 | 63.49 | 324.23.03 | 58.38 | 352.39.25 | 55.12 |
| 23 | 294.50.34 | 63.41 | 325.21.31 | 58.28 | 353.34.35 | 55.10 |
| 24 | 295.54.06 | 63.32 | 326.19.49 | 58.18 | 354.29.43 | 55.08 |
| 25 | 296.57.29 | 63.23 | 327.17.57 | 58.08 | 355.24.49 | 55.06 |
| 26 | 298.00.42 | 63.13 | 328.25.55 | 67.58 | 356.19.53 | 55.04 |
| 27 | 299.03.45 | 63.03 | 329.13.44 | 47.49 | 357.14.56 | 55.03 |
| 28 | 300.06.38 | 62.53 | 330.11.24 | 57.40 | 358.09.58 | 55.02 |
| 29 | 301.09.20 | 62.42 | 331.08.55 | 57.31 | 359.04.59 | 55.01 |
| 30 | 302.11.53 | 62.33 | 332.06.18 | 57.23 | 360.00.00 | 55.01 |
| Distantia nonullarum fixarum Stellarum per sextantes Astronomicos Tychonis Brahe Cælitus exploratæ. | |||
|---|---|---|---|
| Nomina Stellarum. | Distan. | Nomina Stellarum. | Distan. |
| G.M. | G.M. | ||
| Aldeb. & prima ♈︎ | 38.36 | Cor. ♌︎. & Canis min. | 37.19 |
| Aldeb. & secunda ♈︎ | 38.21 | Cor. ♌︎. & cauda ♌︎ | 24.39 |
| Aldeb. & tert. | 35.32 | Coxa & femur ♌︎ | 12.44 |
| Aldeb. & sec. cau. ♈︎ | 26.45 | Coxa & cervix ♌︎ | 8.31 |
| Aldeb. & Calx ♊︎ pr. | 25.53 | Coxa & cor ♌︎ | 17.51 |
| Aldeb. & Propus | 24. 3 | Coxa ♌︎, & spica ♍︎ | 54. 2 |
| Aldeb. & Cap. B ♊︎ | 43.12 | Spica ♍︎, & cervix ♌︎ | 55.12 |
| Lucid. supra Cau. M. ♊︎ | 45. 5 | Spica ♍︎, & cauda ♌︎ | 35. 1 |
| Aldeb. & Luc. pes ♊︎ seq. | 29. 9 | Spica ♍︎ ?? austr. alæ ♍︎ | 14.29 |
| Mer. cap. ♊︎, & Calx ped. | 19.28 | Spica ♍︎, & cor ♏︎ | 45.51 |
| Mer. cap. ♊︎, & ext. pedus | 21.14 | Spica & Chele astr. | 21.22 |
| Bor cap ♊︎, & cor ♌︎ | 40.32 | Spica & Chele bor. | 27.34 |
| Aldeb. & Canis major | 45.57 | Chele Bor, & cap. Oph. | 40.41 |
| Mer. cap. ♊︎ & capella | 34.18 | Bor. lanx & Aufl. lanx ♎︎ | 9. 8 |
| Luc. pes. Or. & Sirius | 23.41 | Spica & B. in sin. m. Oph. | 42.33 |
| Canis major, & Procyon | 25.41 | Spica & B. fron. ♏︎ | 39.26 |
| Luc. pes Or. & Procyon | 38.37 | Spica & Med. fron. ♏︎ | 38.40 |
| Procyon, & Luc. Hydra | 30.20 | Spica & infirm. fron. ♏︎ | 39. 6 |
| Ter ♈︎, & Luc. Pleyad. | 22.56 | Sin. hu ♒︎, & inf. cor. ♑︎ | 19.37 |
| Cor. ♌︎. & ext. pes ♊︎ | 56.26 | Sin. h. ♒︎, & sup. cor ♒︎ | 19.25 |
| Cor. ♌︎. & Calx ped ♊︎ | 54.35 | Dext. h. ♒︎, & vultur | 34.53 |
| Cor. ♌︎. & Mer.cap. ♊︎ | 36.59 | Dext. hu. & sin. hu. ♒︎ | 10. 1 |
| Nomina Stellarum. | Distan. | Nomina Stellarum. | Distan. |
|---|---|---|---|
| G.M. | G.M. | ||
| Dext. hus. ♒︎ & manus ♒︎ | 21.27 | Aldeb. & B. pes Ericht. | 33. 3 |
| Vultur & Luci sup,cor. ♑︎ | 22.25 | Luc. pes Erich. & M. ca. ♊︎ | 30.33 |
| Vultur & mf.cor. ♑︎ | 24.45 | B. pes Erich. M. cap. ♊︎ | 36.23 |
| Vultur & Luc.cande ♑︎ | 38. 5 | Scheat. Peg. Lyra. | 55.30 |
| Vultur & os ♓︎ aust. | 48.16 | Scheat : Med. sin. ala Cyg. | 46. 1 |
| Prac. in ore ♓︎, & os Peg. | 20.41 | Scheat & cap. Cygni. | 46.36 |
| Cap. ♓︎ austr. & vultur | 51.32 | Scheat & pectus Cygni | 35.12 |
| Prac. dorsi ♓︎, & vultur | 53.55 | Polaris & cauda Cygni. | 44.39 |
| Scheat Peg. & Lucida ♈︎ | 41.16 | Luc. cath. & pes Cass. | 13.18 |
| Cap. Andr. & Lucida ♈︎ | 27. 7 | Luc cath. & cing. Cass. | 5.17 |
| Vultur & caud. Cygni | 38. 4 | Polaris & Lyra. | 51.34 |
| Vultur & Lyra | 34. 9 | Polaris & Schedir Cass. | 32.47 |
| Vultur & cap. Cygni | 19.40 | Luc cath. Genu Cass. | 9.41 |
| Vultur & cap. Herc. | 38.32 | Genu Cass. & flexura. | 3.35 |
| Vultur & Luc. m. Oph. | 55.17 | Luc cath. & ♊︎. Cass. | 4.45 |
| Cap. Oph. & B manus ejus | 25.46 | Scheat. & Cingul. | 1.40 |
| Genu Peg. & cap.Andr. | 18.28 | Genu & Cing. | 5.19 |
| Ald. & dext. bu. Or. | 21.23 | Luc. cath. & Schedir. | 4.57 |
| Ter. ♈︎, & sin. hum. Or. | 50.31 | Luc cath. & flexura. | 6.10 |
| Vterque humerius Orio. | 7.30 | Luc. ♈︎. & Luc. cath. | 41.19 |
| Luc. bu. or. & Luc. mă. Coss. | 43. 8 | Luc. ♈︎, & flexura. | 39.10 |
| Ter. ♈︎, & Pr. Balt, Orio. | 55. 7 | Luc. ♈︎, & Genu Cass. | 37.27 |
| Dixt. hu. Or. & M. cap. ♊︎ | 33.16 | Luc. ♈︎, Schedit Cas. | 36.38 |
| Sin. pos. Or. Can. min. | 38.37 | Aldeb. & Genu Cass. | 55.23 |
| Aldeb. & Pr. cing. Or. | 21.49 | Polaris & undecum. Cass. | 26.42 |
| Adeb. & Canis min. | 46.22 | Genu Cass. cap. Andr. | 33.46 |
| Canon Conversionis gr. | Conversio horarum, | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| min. sec. ter. Æquatoris in. | min. sec. ter. in gradus, min. | ||||||||||
| horas, min, sec. & ter. horar. | sec. & ter. æquatoris. | ||||||||||
| G | H.M. | G | H.M. | G | H.M. | H | G | M | G.M. | M | G.M |
| /. | /.//. | /. | /.//. | //. | /.//. | //. | /.//. | ||||
| //. | //.///. | //. | //.///. | ///. | //.///. | ///. | //.///. | ||||
| 1 | 0. 4 | 31 | 2. 4 | 70 | 4.40 | 1 | 15 | 1 | 0.15 | 31 | 7.45 |
| 2 | 0. 8 | 32 | 2. 8 | 80 | 5.20 | 2 | 30 | 2 | 0.30 | 32 | 8. 0 |
| 3 | 0.12 | 33 | 2.12 | 90 | 6. 0 | 3 | 45 | 3 | 0.45 | 33 | 8.15 |
| 4 | 0.16 | 34 | 2.16 | 100 | 6.40 | 4 | 60 | 4 | 1. 0 | 34 | 8.30 |
| 5 | 0.20 | 35 | 2.20 | 110 | 7.20 | 5 | 75 | 5 | 1.15 | 35 | 8.45 |
| 6 | 0.24 | 36 | 2.24 | 120 | 8. 0 | 6 | 90 | 6 | 1.30 | 36 | 9. 0 |
| 7 | 0.28 | 37 | 2.28 | 130 | 8.40 | 7 | 105 | 7 | 1.45 | 37 | 9.15 |
| 8 | 0.32 | 38 | 2.32 | 140 | 9.20 | 8 | 120 | 8 | 2. 0 | 38 | 9.30 |
| 9 | 0.36 | 39 | 2.36 | 150 | 10. 0 | 9 | 135 | 9 | 2.15 | 39 | 9.45 |
| 10 | 0.40 | 40 | 2.40 | 160 | 10.40 | 10 | 150 | 10 | 2.30 | 40 | 10. 0 |
| 11 | 0.44 | 41 | 2.44 | 170 | 11.20 | 11 | 165 | 11 | 2.45 | 41 | 10.15 |
| 12 | 0.48 | 42 | 2.48 | 180 | 12. 0 | 12 | 180 | 12 | 3. 0 | 42 | 10.30 |
| 13 | 0.52 | 43 | 2.52 | 190 | 12.40 | 13 | 195 | 13 | 3.15 | 43 | 10.45 |
| 14 | 0.56 | 44 | 2.56 | 200 | 13.20 | 14 | 210 | 14 | 3.30 | 44 | 11. 0 |
| 15 | 1. 0 | 45 | 3. 0 | 210 | 14. 0 | 15 | 225 | 15 | 3.45 | 45 | 11.15 |
| 16 | 1. 4 | 46 | 3. 4 | 220 | 14.40 | 16 | 240 | 16 | 4. 0 | 46 | 11.30 |
| 17 | 1. 8 | 47 | 3. 8 | 230 | 15.20 | 17 | 255 | 17 | 4.15 | 47 | 11.45 |
| 18 | 1.12 | 48 | 3.12 | 240 | 16. 0 | 18 | 270 | 18 | 4.30 | 48 | 12. 0 |
| 19 | 1.16 | 49 | 3.16 | 250 | 16.40 | 19 | 285 | 19 | 4.45 | 49 | 12.15 |
| 20 | 1.20 | 50 | 3.20 | 260 | 17.20 | 20 | 300 | 20 | 5. 0 | 50 | 12.30 |
| 21 | 1.24 | 51 | 3.24 | 270 | 18. 0 | 21 | 315 | 21 | 5.15 | 51 | 12.45 |
| 22 | 1.28 | 52 | 3.28 | 280 | 18.40 | 22 | 330 | 22 | 5.30 | 52 | 13. 0 |
| 23 | 1.32 | 53 | 3.32 | 290 | 19.20 | 23 | 345 | 23 | 5.45 | 53 | 13.15 |
| 24 | 1.36 | 54 | 3.36 | 300 | 20. 0 | 24 | 360 | 24 | 6. 0 | 54 | 13.30 |
| 25 | 1.40 | 55 | 3.40 | 310 | 20.40 | 25 | 6.15 | 55 | 13.45 | ||
| 26 | 1.44 | 56 | 3.44 | 320 | 21.20 | 26 | 6.30 | 56 | 14. 0 | ||
| 27 | 1.48 | 57 | 3.48 | 330 | 22. 0 | 27 | 6.45 | 57 | 14.15 | ||
| 28 | 1.52 | 58 | 3.52 | 340 | 22.40 | 28 | 7. 0 | 58 | 14.30 | ||
| 29 | 1.56 | 59 | 3.56 | 350 | 23.20 | 29 | 7.15 | 59 | 14.45 | ||
| 30 | 2. 0 | 60 | 4. 0 | 360 | 24. 0 | 30 | 7.30 | 60 | 15. 0 | ||
| Tabvla contiens 100 selectarum Stelarum Ascensiones Rectas & Declinationes, ad Annos com- pletos, 1600 & 1700. unà cum earundem intercedente differentia. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Nomina Stel- larum. | Anno 1600. | Differentia. | Anno 1700. | |||||
| Asc. R. | Decl. | Asc. R | Decl. | Asc. R. | Decl. | |||
| G M. | G. M | G. M. | M | G. M. | G. M. | |||
| Scheder Cassiopeæ | 4,36 | 54,21 | B. | 1,22 | 34 | A | 5,58 | 54,55 |
| Stella Polaris | 5,47 | 87,09 | B. | 1,59 | 34 | A. | 9,46 | 87,43 |
| Austr. cauda. Cete | 5,51 | 20,12 | A. | 2,17 | 34 | S. | 7,08 | 19,38 |
| Flexura Cassiop. | 8,21 | 58,33 | B. | 1,27 | 34 | A. | 9,48 | 59,07 |
| Cingul. Andrŏ. | 11,50 | 33,32 | B. | 1,23 | 33 | A. | 13,13 | 34,05 |
| Genu Cassiopeæ | 15,03 | 58,07 | B. | 1,35 | 33 | A. | 16,38 | 58,40 |
| Præced. cornu ♈︎ | 22,56 | 17,19 | B. | 1,23 | 31 | A. | 24,19 | 17,50 |
| Venter Cete | 22,59 | 12,16 | A. | 1,15 | 31 | S. | 24,14 | 11,45 |
| Sequens cornu ♈︎ | 23,10 | 18,50 | B. | 1,22 | 31 | A. | 24,32 | 19,21 |
| Austr. pes Andrō. | 24,55 | 40,23 | B. | 1,29 | 30 | A. | 26,24 | 40,53 |
| Nidus lini ♓︎ | 25,22 | 0,50 | B. | 1,18 | 30 | A. | 26,40 | 1,20 |
| Lucida ♈︎ | 26,13 | 21,33 | B. | 1,25 | 30 | A. | 27,38 | 22,03 |
| Luc. mand. Cete | 40,25 | 2,29 | B. | 1,15 | 25 | A. | 41,40 | 2,54 |
| Caput Medusa | 40,38 | 39,22 | B. | 1,37 | 25 | A. | 42,15 | 39,47 |
| Lucid. lat. Persei | 44,02 | 48,22 | B. | 1,28 | 21 | A. | 45,30 | 48,43 |
| Lucida Pleiad ♉︎ | 50,57 | 22,49 | B. | 1,29 | 21 | A. | 52,26 | 23,10 |
| Insima Hyad. ♉︎ | 59,16 | 14,37 | B. | 1,25 | 17 | A. | 60,41 | 14,54 |
| Boreus oculus ♉︎ | 61,21 | 18,14 | B. | 1,24 | 17 | A. | 62,45 | 18,31 |
| Aldebran ♉︎. | 63,16 | 15,38 | B. | 1,26 | 15 | A. | 64,43 | 15,53 |
| Capella | 71,49 | 45,30 | B. | 1,49 | 10 | A. | 73,38 | 45,40 |
| Lucidus pes Orio | 73,51 | 8,43 | A. | 1,15 | 9 | S. | 75,07 | 8,33 |
| Boreale cornu ♉︎ | 75,16 | 28,12 | B. | 1,37 | 8 | A. | 76,53 | 28,20 |
| Nomina Stel- larum. | Anno 1600. | Differentia. | Anno 1700. | |||||
| Asc. R. | Decl. | Asc. R | Decl. | Asc. R. | Decl. | |||
| G M. | G. M | G. M. | M | G. M. | G. M. | |||
| Prac. hum. Orio. | 75,58 | 5,55 | B | 1,19 | 8 | A | 77,17 | 6,03 |
| Femur Leporu. | 77,48 | 21,06 | A | 1,05 | 7 | S | 78,53 | 20,59 |
| Prac. Balter. Orio. | 77,58 | 0,39 | A | 1,17 | 7 | S | 79,15 | 0,32 |
| Supr. caps. Orio. | 78,21 | 9,36 | B | 1,22 | 7 | A | 79,43 | 9,43 |
| Austrae corn ♉︎ | 78,26 | 20,51 | B | 1,31 | 7 | A | 79,57 | 20,58 |
| Media Balt. Orio. | 79,01 | 1,30 | A | 1,17 | 6 | S | 80,18 | 1,24 |
| Infer. Balt. Orio. | 80,10 | 2,12 | A | 1,16 | 5 | S | 81,26 | 2,07 |
| Dext. hu. Aurig. | 82,40 | 44,50 | B | 1,55 | 4 | A | 84,35 | 44,54 |
| Beguēs hu. Orio. | 83,26 | 7,16 | B | 1,22 | 4 | A | 84,48 | 7,20 |
| Lucida?? Pes ♊︎. | 93,38 | 16,40 | B | 1,28 | 2 | S | 95,06 | 16,38 |
| Canis maj. Sirius | 96,53 | 16,11 | A | 1,07 | 4 | A | 98,00 | 16,15 |
| Super. capus ♊︎ | 107,09 | 32,41 | B | 1,44 | 11 | S | 108,53 | 32,30 |
| Canis ?en. Proc. | 109,37 | 6,12 | B | 1,20 | 12 | S | 110,57 | 6,00 |
| Infer. capus ♊︎ | 110,13 | 28,55 | B | 1,34 | 12 | S | 111,47 | 28,43 |
| Luc. in Puppi Na. | 117,39 | 23,11 | A | 1,04 | 15 | A | 118,43 | 23,26 |
| Præcape ♋︎ | 124,20 | 21,02 | B | 1,28 | 19 | S | 125,48 | 20,43 |
| Borcus Asell. ♋︎ | 124,58 | 22,51 | B | 1,30 | 20 | S | 126,28 | 22,31 |
| Austr. Asell. ♋︎ | 125,27 | 19,35 | B | 1,27 | 20 | S | 126,54 | 19,15 |
| Cor Hydra | 137,01 | 6,57 | A | 1,15 | 25 | A | 138,16 | 7,22 |
| Infima cervic. ♌︎ | 146,22 | 18,42 | B | 1,28 | 28 | S | 147,10 | 18,14 |
| Cor ♌︎ Balsiliscus | 146,45 | 13,53 | B | 1,22 | 28 | S | 148,08 | 13,25 |
| Supre. cervic. ♌︎ | 148,33 | 25,23 | B | 1,28 | 29 | S | 150,01 | 24,54 |
| Media cervic. ♌︎ | 149,25 | 21,50 | B | 1,25 | 29 | S | 150,51 | 21,21 |
| Inf. pr. □ ur. ma. | 159,12 | 58,31 | B | 1,37 | 32 | S | 160,49 | 57,59 |
| Super. □ Dubh. | 159,37 | 63,54 | B | 1,41 | 32 | S | 161,18 | 63,22 |
| Nomina Stel- larum. | Anno 1600. | Differentia. | Anno 1700. | |||||
| Asc. R. | Decl. | Asc. R | Decl. | Asc. R. | Decl. | |||
| G M. | G. M | G. M. | M | G. M. | G. M. | |||
| Lucid. lumbi ♌︎ | 163,10 | 22,43 | B | 1,27 | 34 | S | 164,37 | 22,09 |
| Cauda ♌︎ | 172,09 | 16,59 | B | 1,19 | 34 | S | 173,28 | 16,25 |
| Inf. seq. □ ur. ma | 173,03 | 55,57 | B | 1,23 | 34 | S | 174,26 | 55,23 |
| Superior □ seq. | 178,50 | 59,15 | B | 1,20 | 34 | S | 180,10 | 58,41 |
| Cingulum ♍︎ | 188,53 | 5,37 | B | 1,18 | 34 | S | 190,11 | 5,03 |
| Rad. cau. ur. ma. | 189,01 | 58,10 | B | 1,09 | 33 | S | 190,10 | 57,37 |
| Vindemiatrix ♍︎ | 190,36 | 13,08 | B | 1,17 | 33 | S | 191,53 | 12,35 |
| Spica ♍︎ | 196,04 | 9,01 | A | 1,19 | 32 | A | 197,23 | 9,33 |
| Pen. cau. ur. ma. | 196,54 | 57,03 | B | 1,03 | 32 | S | 197,57 | 56,31 |
| Vicam. cau. ejus. | 202,54 | 51,22 | B | 1,02 | 31 | S | 203,56 | 50,51 |
| Arcturus. | 209,23 | 21,18 | B | 1,11 | 29 | S | 210,34 | 20,49 |
| Sinist. hu. Booia | 214,02 | 40,03 | B | 1,02 | 27 | S | 215,04 | 39,36 |
| Astrin. lanx. ♒︎ | 217,14 | 14,18 | A | 1,23 | 27 | A | 218,37 | 14,45 |
| Boreas lanx ♒︎ | 223,54 | 7,50 | A | 1,21 | 24 | A | 225,16 | 8,14 |
| Lucida corone | 229,26 | 28,06 | B | 1,05 | 21 | S | 230,31 | 27,45 |
| Colli serpentes | 231,12 | 7,46 | B | 1,15 | 21 | S | 232,27 | 7,25 |
| Boreal. frontu ♏︎ | 235,34 | 18,38 | A | 1,28 | 19 | A | 237,02 | 18,57 |
| Sin. man. Phiu | 238,25 | 2,37 | A | 1,23 | 18 | A | 239,48 | 2,55 |
| Cor ♍︎ Antares | 241,18 | 25,26 | A | 1,32 | 16 | A | 242,50 | 25,42 |
| Dext. hu- Hercu. | 243,15 | 22,27 | B | 1,05 | 15 | S | 244,20 | 22,12 |
| Sinis. genu Ophi. | 243,49 | 9,39 | A | 1,23 | 15 | A | 245,12 | 9,54 |
| Dext. Genu ejus. | 251,50 | 15,07 | A | 0,50 | 10 | A | 252,40 | 15,17 |
| Caput Hercules | 254,06 | 14,55 | B | 1,08 | 8 | S | 255,14 | 14,47 |
| Sinist. hu. Herc. | 254,40 | 25,22 | B | 0,52 | 8 | S | 255,32 | 25,14 |
| Caput Opheuchi | 259,05 | 13,56 | B | 1,11 | 7 | S | 260,16 | 13,49 |
| Dext. hu. Ophi | 260,56 | 4,49 | B | 1,13 | 5 | S | 262,09 | 4,44 |
| Nomina Stel- larum. | Anno 1600. | Differentia. | Anno 1700. | |||||
| Asc. R. | Decl. | Asc. R | Decl. | Asc. R. | Decl. | |||
| G M. | G. M | G. M. | M | G. M. | G. M. | |||
| Lucid. cap. Drac. | 266,52 | 51,37 | B. | 0,35 | 2 | S | 267,27 | 51,35 |
| Lucida Lyra | 275,52 | 38,28 | B. | 0,50 | 4 | A | 276,42 | 38,32 |
| Orient. Cap ♐︎ | 281,32 | 21,35 | A. | 1,31 | 8 | S | 283,03 | 21,27 |
| Cauda Vulturu. | 281,47 | 13,20 | B. | 1,13 | 8 | A | 283,00 | 13,28 |
| Rostrum Cygni | 288,40 | 27,10 | B. | 1,01 | 11 | A | 289,41 | 27,21 |
| Lucida Vulturu | 292,49 | 7,54 | B. | 1,17 | 13 | A | 294,06 | 8,07 |
| Super. ala Cygni | 293,10 | 44,12 | B. | 0,48 | 14 | A | 293,58 | 44,26 |
| Super. cornu ♑︎ | 298,57 | 13,40 | A. | 1,25 | 16 | S | 300,22 | 13,24 |
| Infer. cornu ♑︎ | 299,39 | 15,57 | A. | 1,27 | 17 | S | 301,06 | 15,40 |
| Pectus Cygni | 302,01 | 39,01 | B. | 0,53 | 18 | A | 302,55 | 39,19 |
| Sinistra man. ♒︎ | 306,32 | 10,53 | A. | 1,16 | 19 | S | 307,48 | 10,34 |
| Cauda Cygni . | 306,57 | 43,53 | B. | 0,51 | 20 | A | 307,49 | 44,14 |
| Infer. ala Cygni | 307,31 | 32,30 | B. | 1,00 | 21 | A | 308,31 | 32,51 |
| Sinister hum. ♒︎ | 317,37 | 7,15 | A. | 1,21 | 26 | S | 318,58 | 6,49 |
| Praced. cauda ♑︎ | 319,28 | 18,21 | A. | 1,26 | 26 | S | 320,44 | 17,55 |
| Cingul. Cep?es | 320,46 | 68,50 | B. | 0,22 | 26 | A | 321,08 | 69,16 |
| Os Pegasi. | 321,10 | 8,05 | B. | 1,18 | 26 | A | 322,28 | 8,31 |
| Sequens caud. ♑︎ | 321,16 | 17,51 | A. | 1,25 | 27 | S | 322,41 | 17,24 |
| Dexter hum. ♒︎ | 326,19 | 2,13 | A. | 1,20 | 29 | S | 327,39 | 1,44 |
| Fomahans ♒︎ | 338,46 | 31,39 | A. | 1,25 | 31 | S | 340,11 | 31,08 |
| Scheat Pegasi. | 341,09 | 25,56 | B. | 1,12 | 32 | A | 342,21 | 26,28 |
| Marchab. Pegasi. | 341,15 | 13,05 | B. | 1,15 | 32 | A | 342,30 | 13,37 |
| Occipus ♓︎ austr. | 344,09 | 1,07 | B. | 1,17 | 33 | A | 345,26 | 1,40 |
| Caput Androm. | 356,59 | 26,54 | B. | 1,17 | 34 | A | 358,16 | 27,28 |
| Lucid. cath. Cass. | 357,05 | 56,58 | B. | 1,15 | 34 | A | 358,20 | 57,32 |
| Extrem. ala Peg. | 358,14 | 12,58 | B. | 1,16 | 34 | A | 359,30 | 13,32 |
| Boreal cau. Cete | 359,49 | 11,01 | A. | 1,18 | 34 | S | 361,07 | 10,27 |
| Tabvula continens Prædictarum 10 Stella- rum Longitudines & Latitudines ad annum completum 1600. | |||||
| Nomina Stellarum. | Longit. | Latit. | Magn. | ||
| S | G. M | G. M. | B | ||
| Stella Polaris. | ♊︎ | 23.02 | 56.02 | B | 2 |
| Superior □ Ursa ma. Dubhe. | ♌︎ | 9.34 | 49.40 | B | 2 |
| Inf. Preced. □ Ursa ma. | ♌︎ | 13.43 | 45.03 | B | 2 |
| Infer. Seq. □ Ursa ma. | ♌︎ | 24.45 | 47.06 | B | 2 |
| Superior seq. Ejusdem. | ♌︎ | 25.25 | 51.37 | B | 2 |
| Prima seu radix cauda Urs. | ♍︎ | 3.00 | 54.18 | B | 2 |
| Penult. Cauda Ursa ma. | ♍︎ | 9.56 | 56.22 | B | 2 |
| Ultima cauda Ursa ma. | ♍︎ | 21.12 | 54.25 | B | 2 |
| Lucida capitis Dracon. | ♐︎ | 22.24 | 75.03 | B | 3 |
| Qua flexuram proximè sequitur. | ♍︎ | 2.10 | 66.36 | B | 2 |
| Cingulum Caphei. | ♉︎ | 0.13 | 71.07 | B | 3 |
| Arcturus. | ♎︎ | 18.39 | 31.02 | B | 1 |
| Sinister humerus Bootis. | ♎︎ | 13.05 | 49.33 | B | 3 |
| Lucida Corona. | ♏︎ | 6.38 | 44.23 | B | 2 |
| Dexter humerus Herculis. | ♏︎ | 25.27 | 42.48 | B | 3 |
| Sinister humerus ejusdem. | ♐︎ | 9.10 | 47.47 | B | 3 |
| Lucida Lyra. | ♑︎ | 9.43 | 61.47 | B | 1 |
| Rostrum Cygni. | ♑︎ | 25.44 | 49.02 | B | 3 |
| Pectus Cygni. | ♒︎ | 19.25 | 57.09 | B | 3 |
| Superior ala Cygni. | ♒︎ | 10.53 | 64.28 | B | 3 |
| Inferior ala ejusdem. | ♒︎ | 22.09 | 49.26 | B | 3 |
| Cauda Cygni. | ♒︎ | 29.53 | 59.56 | B | 2 |
| Schedir Cassiopea. | ♉︎ | 2.47 | 46.35 | B | 3 |
| Nomina Stellarum. | Longit. | Latit. | Magn. | ||
| S | G. M | G. M. | B | ||
| Flexura Cassiopea. | ♉︎ | 8.27 | 48.45 | B | 3 |
| Genu Cassiopea. | ♉︎ | 12.21 | 46.22 | B | 3 |
| In crure Cassiop. | ♉︎ | 19.13 | 47.29 | B | 3 |
| Lucida cathedra Cassio. | ♈︎ | 29.35 | 51.14 | B | 3 |
| Lucidum latus Persei. | ♉︎ | 26.17 | 30.05 | B | 2 |
| Caput Medusa, Algol. | ♉︎ | 20.37 | 22.22 | B | 2 |
| Capella. | ♊︎ | 16.16 | 22.51 | B | 1 |
| Dexter hum. Auriga, | ♊︎ | 25.52 | 21.27 | B | 2 |
| Caput Ophiuchi, | ♐︎ | 16.50 | 35.57 | B | 3 |
| Dextra hum. Sup. Oph. | ♐︎ | 19.54 | 28.01 | B | 3 |
| Sinistre manus Bor. Oph. | ♏︎ | 26.44 | 17.19 | B | 3 |
| Sinistrum Genu Ophruchi, | ♐︎ | 3.39 | 11.30 | B | 3 |
| Dextrum Genu Ophruchi, | ♐︎ | 12.24 | 7.18 | B | 3 |
| Lucida colli serpensis, | ♏︎ | 16.30 | 25.35 | B | 2 |
| Lucida vulturis, | ♑︎ | 26.09 | 29.21 | B | 2 |
| Cauda vulturis, | ♑︎ | 14.15 | 36.16 | B | 3 |
| Os Pegasi, | ♒︎ | 26.22 | 22.07 | B | 3 |
| Marchab Pegasi, | ♓︎ | 17.56 | 19.26 | B | 2 |
| Scheas Pegasi, | ♓︎ | 23.49 | 31.07 | B | 2 |
| Extrema ala Pegasi, | ♈︎ | 3.38 | 12.35 | B | 2 |
| Caput Andromeda, | ♈︎ | 8.47 | 25.42 | B | 2 |
| Cingulum Androm. | ♈︎ | 24.49 | 25.59 | B | 2 |
| Australis pes Androm. | ♉︎ | 8.39 | 27.46 | B | 2 |
| Lucida ♈︎ | ♉︎ | 2.06 | 9.57 | B | 3 |
| Preced. Cornu ♈︎, | ♈︎ | 27.37 | 7.08 | B | 4 |
| Sequens cornu ♈︎, | ♈︎ | 28.23 | 8.29 | B | 4 |
| Oculus ♉︎ Aldebran. | ♊︎ | 4.12 | 5.31 | A | 1 |
| Nomina Stellarum. | Longit. | Latit. | Magn. | ||
| S | G. M | G. M. | B | ||
| Oculus Boresu ♉︎ | ♊︎ | 2.53 | 2.36 | A | ? |
| Boreale cornu ♉︎ | ♊︎ | 16.59 | 5.20 | B | ? |
| Australe cornu ♉︎ | ♊︎ | 19.12 | 2.14 | A | ? |
| Lucida Pleyadum ♉︎ | ♉︎ | 24.24 | 4.00 | B | ? |
| Ingfima Hyadum ♉︎ | ♊︎ | 0.12 | 5.46 | A | ? |
| Caput superius ♊︎ | ♋︎ | 14.41 | 10.02 | B | ? |
| Caput inferius ♊︎ | ♋︎ | 17.43 | 6.38 | B | ? |
| Lucidus pes ♊︎ | ♋︎ | 3.31 | 6.48 | A | ? |
| Præcipe ♋︎ | ♌︎ | 1.46 | 1.14 | B | ? |
| Brachium austrinum ♋︎ | ♌︎ | 8.03 | 5.08 | A | ? |
| Asellus Boreus ♋︎ | ♌︎ | 1.57 | 3.08 | B | ? |
| Asellus Astralis ♋︎ | ♌︎ | 3.08 | 0.04 | A | ? |
| Cor ♌︎ Basiliscus, Regulus. | ♌︎ | 24.27 | 0.26 | B | ? |
| Cauda ♌︎ | ♍︎ | 16.03 | 12.18 | B | ? |
| Suprem. Cervicis ♌︎ | ♌︎ | 21.57 | 11.50 | B | ? |
| Media cervicis ♌︎ | ♌︎ | 23.59 | 8.37 | B | ? |
| Infirm. Cervicis ♌︎ | ♌︎ | 22.20 | 4.52 | B | ? |
| Lucida lumbi, ♌︎ | ♍︎ | 5.41 | 14.20 | B | ? |
| Spica ♍︎ | ♎︎ | 18.16 | 1.59 | A | ? |
| Cingulum ♍︎ | ♎︎ | 5.55 | 8.41 | B | ? |
| Vindemiatrix ♍︎ | ♎︎ | 4.23 | 16.15 | B | ? |
| Austrina lanx ♎︎ | ♏︎ | 9.31 | 0.26 | B | ? |
| Borea lanx ♎︎ | ♏︎ | 13.48 | 8.35 | B | ? |
| Cor ♏︎, Antares. | ♐︎ | 4.13 | 4.27 | A | ? |
| Borealu frontu ♏︎ | ♏︎ | 27.36 | 1.05 | B | ? |
| Orientalis cap. ♐︎ | ♑︎ | 10.43 | 1.31 | B | ? |
| Superius cornu ♑︎ | ♑︎ | 28.18 | 7.02 | B | ? |
| Nomina Stellarum. | Longit. | Latit. | Magn. | ||
| S | G. M | G. M. | B | ||
| Inferius Cornu ♑︎ | ♑︎ | 28.31 | 4.41 | B | 3 |
| Præced. Cauda ♑︎ | ♒︎ | 16.14 | 2.26 | A | 3 |
| Seq. Cauda ♑︎ | ♒︎ | 18.00 | 2.29 | A | 3 |
| Fomabant ♒︎ | ♒︎ | 28.11 | 21.00 | A | 1 |
| Sinist, humerus ♒︎ | ♒︎ | 17.51 | 8.42 | B | 3 |
| Dexter hum. ♒︎ | ♒︎ | 27.49 | 10.42 | B | 3 |
| Sinistra manus ♒︎ | ♒︎ | 6.12 | 8.10 | B | 4 |
| Occiput Australis ♓︎ | ♓︎ | 15.50 | 7.17 | B | 4 |
| Nodus lini ♓︎ | ♈︎ | 23.47 | 9.04 | A | 3 |
| Lucida Mandib. Cete. | ♉︎ | 8.47 | 12.37 | A | 2 |
| venter Cete. | ♈︎ | 12.25 | 25.01 | A | 4 |
| Australis Cauda Cete. | ♓︎ | 25.56 | 20.47 | A | 2 |
| Borealis Cauda Cete. | ♓︎ | 25.23 | 10.01 | A | 3 |
| Suprema Capitis Orio. | ♊︎ | 18.11 | 13.26 | A | 4 |
| Præced. Hum. Orion. | ♊︎ | 15.23 | 16.53 | A | 2 |
| Seq. Humerus Orionis. | ♊︎ | 13.12 | 17.06 | A | 2 |
| Preced. Baltei Orio. | ♊︎ | 16.50 | 23.38 | A | 2 |
| Media Baltiei Orion. | ♊︎ | 17.54 | 24.33 | A | 2 |
| Infer. Seu seq. Balties Orio. | ♊︎ | 19.06 | 25.21 | A | 2 |
| Lucidus Pes Orio. Regel. | ♊︎ | 16.17 | 31.11 | A | 1 |
| Femur Leporis. | ♊︎ | 21.36 | 44.18 | A | 3 |
| Canis major. Sirius. | ♋︎ | 8.35 | 39.30 | A | 1 |
| Ad annulum Collarii ejusdem. | ♋︎ | 1.42 | 41.18 | A | 2 |
| Canis minor. Procyon. | ♋︎ | 20.18 | 15.57 | A | 2 |
| In collo Canis min. | ♋︎ | 16.39 | 13.33 | A | 3 |
| Cor Hydra. | ♌︎ | 21.45 | 22.24 | A | 1 |
| Lucida in puppi Navis. | ♌︎ | 5.53 | 43.18 | A | 3 |
Notandum hic est Longitudines Stellarum non semper manere easdem, sed quotannis augeri per 51. scr. sec. quod crebris & accuratis observationibus expertus est Tycho Brahe. quolibet ergò mense per 4". & qualibet septimana per 1". mutantur. Et quia hic motus sit circa polos Zodiaci, ideoque Latitudines Stellarum non variantur.
Jam quamvis præcedens Tabula eas duntaxat Longitudines ostendat, quas Stellæ anno 1600. habuerunt ; nihilominus tamen ad alium quemcunq; annum propositum earundem Longitudines inde colligere licet, modo teneatur sequens
Regula.
Annum quæcunque oblatum confer cum anno radicali 1600. minoremque à majori aufer, residuum (quoad annos completos) multiplica per 51" menses verò si qui fuerint, per 4". producta adde, & in scr. prim. & gradus (quando id fieri potest) converte, hunc numerum inventam, si annus oblatus, anno radicali fuerit minor ; aufer à numero stellæ, cujus longitudinem quæris, in tabula notato. Si vero anus propositus, radicali fuerit major ; numerus inventus addendus erit. Atque sic ad quodcunque tempus oblatum, vera longitudo cujuscunque stellæ in Tabula positæ, cognosci postest.
Exemplum.
Quæratur quamnam Sirius habuerat longitudinem Anno 1572. completo ? Subtrahatur
annus oblatus ab Anno radicali 1600. manebunt 28. quæ per 51". multiplicata, faciunt 1428", id est, (per 60' reducta) 23'48". quæ à numero in tabula posito sc. 8.35'.30". sunt auferenda, manebit Longitudo Syrii ad tempus datum. 8.11'.42".
Aliud Exemplum.
Lubet scire quam habebit longitudinem cor Hydræ 15 Julij St. N. Anni currentis 1643 ? Ab hoc anno itaque proposito subtrahatur annus radicalis 1600, manebunt 42 anni, & 7 menses (seu 28 septimanæ) multiplicantur jam, juxta regulam, 42 per 51". factus erit 2142". item 7. per 4". fiunt 28". quæ producta simul faciunt 2170". id est, 36'.10". hic numerus ad numerum in Tabula positum, (scil. 21.45'.30".) est addendus, quia annus propositus, anno radicali est major, & erit longitudo quæsita, 22.21'.40". Nec aliter in omnibus aliis eemplis oblatis est procedendum.
PARTIS PRIMAÆ.
Capita.
| I. | De Adornatione Lìmbi. | Pag. 1 |
|---|---|---|
| II. | De Astrolabii divisione. | 3 |
| III. | De Divisionis examine. | 4 |
| IV. | De Numeris. | 6 |
| V. | De Dioptris. | 10 |
| VI. | De aliis modis instr. dividendi. | 13 |
| VII. | De Transportatore. | 14. |
Problemata.
| I. | Altitudinem rei accessibilis metiri. | 16 |
|---|---|---|
| II. | Partem altitudinis access. investigare. | 19 |
| III. | Altitudinem rei accessibilis per basim sursum vergentem explorare. | 20 |
| IV. | Alt. rei acces. ex basi deorsum vergente metiri | 21 |
| V. | Partem altit. rei accessibilis per basim obliquam inquirere. | ibid. |
| VI. | Altit. rei inaccessibilis per duas stationes ex basi recta invenire. | 22 |
| VII. | Partem altit. inaccessibilis investigare. | 24 |
| VIII. | Altit. inaccessibilem ex alia altit. cognosere. | 25 |
| IX. | Altitudinem inaccessibilem ex parte acclivitatis montis inquirere. | 26 |
| X. | Altit. inaccess. in monte positam, ex alia altitudine etiam in monte posita metiri. | 27 |
| XI. | Altitudinem, cujus basis non videtur ex basi transversa metri. | 28 |
| XII. | Altitudinem metiri per basim transversam si basis ejus appareat. | 30 |
|---|---|---|
| XII. | Longitudinem alicujus rei rectilineæ invenire, cujus pars tantum supra aliam altitudinem eminet. | 31 |
| XIV. | Altitudinem montis ex altitudine turris in eo posita invenire. | 33 |
| XV. | Altitud. turris ax alia turri in eadem montis obliquitate posita deprehendere. | 34 |
| XVI. | Altitudinem montis ex distantia aliqua in vertice montis data, investigare. | 35 |
| XVII. | Distantiam duorum locorum invenire. | 36 |
| XVIII. | Distantias plurium locorum in eadem linea recta dispositorum invenire. | 37 |
| XIX. | Distantiam duorum locorum, ex basi transversa reperire. | 39 |
| XX. | Distantiam duorum locorum ex basi retrocadente inquirere. | 40 |
| XXI. | Distantiam duorum locorum inquirere si dantur libera stationes. | 41 |
| XXII. | Distant. duorum vel plurium locorum in linea recta invenire, si prima statio in eorum linea datur. | 42 |
| XXIII. | Idem ex basi obliqua prestare. | 43 |
| XXIV. | Dist. Navis ab aggere explorare. | 44 |
| XXV. | Dist. navium à se invicem experiri. | ibid. |
| XXVI. | Profunditatem putei notam reddere. | 45 |
| XXVII. | Tractum lineæ rectæ per varia impedimenta transeuntis, datis duobus punctis, invenire. | 46 |
| XXVIII. | Figuras rectilineas ex charta in campum transferre. | 74(sic) |
|---|---|---|
| XXIX. | Urbes & fortalitia è campo in chartam delineare. | 49 |
| XXX. | Mappas Topographicas conficere. | 51 |
| XXXI. | Altitudinem lapsus aquarum experiri. | 53 |
PARTIS ALTERIUS.
Capita.
| I. | De Turricula. | 55 |
|---|---|---|
| II. | De Fabrica ipsius Quadrantis. | 57 |
| III. | De hujus Instrumenti Divisione. | 58 |
| IV. | De Dioptris. | 63 |
| V. | De illis rebus quibus Instrumentum sustentatur. | 66 |
| VI. | De Circulo Azimuthali. | 67 |
Problemata.
| I. | Lineam Meridianam invenire. | 68 |
|---|---|---|
| II. | Elevationem Poli per Stellas circumpolares invenire: | 70 |
| III. | Altitudinem Solis, Lunæ vel alterius sideris deprehendere. | 71 |
| IV. | Obliquitatem Zodiaci investigare. | 72 |
| V. | Locum Solis in Ecliptica invenire. | 73 |
| VI. | Declinationem Stellarum invenire. | 76 |
| VII. | Ascensionem rectam Solis invenire. | ibid. |
| VIII. | Asc. rectam stellarum investigare. | 77 |
|---|---|---|
| IX. | Data asc. recta & decl. stellarum, earundem Latitudinem & Longit. invenire. | ibid. |
| X. | Data Longitudine, & Latit. Asc. rectam & declinationem invenire. | 81 |
| XI. | Distantias Stellarum invenire. | 82 |
| XII. | Longitudinem & Latit. Planetæ, vel alterius cujusdam novi syderis, ex duarum stellarum distantia, Longitudine ac Latit. cognitis invenire. | 83 |
| XIII. | Datis duarum stellarum in eodem Azimutho existentium distantia, & alterutrius altitudine; elevationem Poli invenire. | 85 |
| XIV. | Data declinatione duarum Stellarum in eodem cognito Almucantharat sitarum ; elevationem poli invenire. | 86 |
| XV. | Data temporis articulo, cum Phænomeni novi altitudine, & Azimuthali gradu simul observandis : datur ejus asc. recta atque decl. ideoque etiam ejus Longitudine & Latitudo. | 87 |
| XVI. | Data altitudine Solis, ejusque declin. cum elevatione Poli ; datur momentum temporis in horis ac minutis correspondens ; & contra. | 89 |
| XVII. | Data ascensione recta Solis, unà cum ascensione reca ac declin. alicujus Stellæ, ejusque altitudine ex observatione, sub certa elevat. Poli ; datur tempus nocturnum correspondens. | 92 |
| XVIII. | Data Phænomeni circa Polum mundi semper conspicui utraque altitudine meridiana ; datur aggregata in utraque altitudini parallaxis si quam habuerit, vel differentia. | 93 |
|---|---|---|
| XIX. | Data Parallaxiam summa, vel earum differentia ; ipsas parallaxes invenire. | 97 |
| XX. | Parallaxes Phænomeni non semper conspic(?)i invenire. | 100 |
| XXI. | Tabulam Refractionum Solis construere. | 101 |